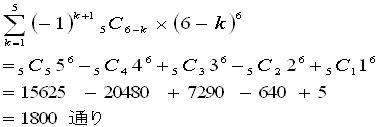NO.1688 フーリエ級数(1) 2007.9.24 水の流れ
第１９７回数学的な応募問題
皆さん、ゼーター関数をご存知ですか。今回の問題はフーリエ級数とζ（２）の関係です。
注：この記事に関する投稿の掲載は、２００７年１０月１５日以降とします。
NO.1687 硬貨の両替(2) 2007.9.24 夜ふかしのつらいおじさん
(1)
50n円を、50円玉と10円玉で支払う方法を考えます。
50円玉の枚数を考え残りを10円玉で調整すると考えます。
50円玉を使わない場合もあるので、(n+1)通りあります。
この場合の数を、ｆ50(n)で表すことにします。
つまり、f50(n)=n+1
(2)
100n円を、100円玉と50円玉と10円玉で支払う方法を考えます。
100円玉を、k枚使ったとします。
残り100(n-k)円を50円玉と10円玉で支払えばよいわけです。
100(n-k)＝50・2(n-k)なので、(1)の結果から、
f50(2(n-k))通りの支払い方があります。
kは0からnまでの場合があるので
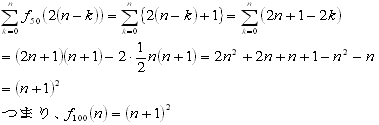
(3)
500n円を、500円玉、100円玉、50円玉、10円玉で支払う方法を考えます。
500円玉を、k枚使ったとします。
残り500(n-k)円を100円玉と50円玉と10円玉で支払えばよいわけです。
500(n-k)＝100・5(n-k)なので、(2)の結果から、
f100(5(n-k))通りの支払い方があります。
kは0からnまでの場合があるので
NO.1686 硬貨の両替(1) 2007.9.3 水の流れ
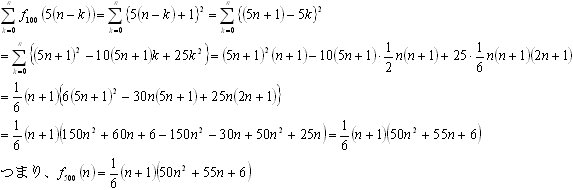
問題の一部修正 9/3 21:00
第１９６回数学的な応募問題
皆さん、次のような両替の問題を考えました。よろしくお願いします。
問題１：５０ｎ円を５０円硬貨、１０円硬貨だけで集金する方法は何通りあるか。ｎで表せ。
問題２：１００ｎ円を、１００円硬貨、５０円硬貨、１１０円硬貨だけで集金する方法は何通りあるか。ｎで表せ。
問題３：５００ｎ円を、５００円硬貨、１００円硬貨、５０円硬貨、１０円硬貨だけで集金する方法は何通りあるか。ｎで表せ。
以上の問題で、ｎは自然数を表す。
＜ヒント：解法が分からなかったら、ｎ＝１、２、３、・・・と実際に数えていき、
漸化式を作ってください。＞
注：この記事に関する投稿の掲載は、２００７年９月２４日以降とします。
NO.1685 分配問題 (2) 2007.9.3 夜ふかしのつらいおじさん
問題１
一つのボールはAかBのどちらかの箱に入るのですべての入れ方は、２5通りあります。
そのうち、Aだけ、Bだけの入り方の２通りを引けばよいので
２5−２
＝３０通り
問題２
一つのボールはA、B、Cのどれかに入るのですべての入れ方は、３5通りあります。
A、B、Cのうち２つの箱の選び方は、3Ｃ2通り、
２つの箱への入れ方は、問題１より、２5−２通り
A、B、Cのうち１つの箱の選び方は、3Ｃ1通り、
１つの箱への入れ方は、１通りなので
３5−3Ｃ2×(２5−２)−3Ｃ1×１
＝２４３−３×３０−３
＝１５０通り
問題３
問題２と同様の考え方をして、少し整理の方法を変えます。
４5−4Ｃ3×｛３5−3Ｃ2×(２5−２)−3Ｃ1×１｝−4Ｃ2×(２5−２)−4Ｃ1×１5
＝１×４5−４×３5＋６×２5−４×１5
＝4Ｃ4×４5−4Ｃ3×３5＋4Ｃ2×２5−4Ｃ1×１5
＝4Ｃ4×４5−4Ｃ3×３5＋4Ｃ2×２5−4Ｃ1×１5・・・・・・（１）
＝１×１０２４−４×２４３＋６×３２−４×１
＝２４０通り
問題４
問題３の(1)の式から考えて
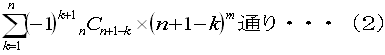
問題３を例に具体的に考えます。
4Ｃ4×４5−4Ｃ3×３5＋4Ｃ2×２5−4Ｃ1×１5・・・・・・（１）
箱を、Ａ、Ｂ、Ｃ、Ｄとします。
（１）の第１項で使われる箱は
ＡＢＣＤ
ＡＢＣ、ＡＢＤ、ＡＣＤ、ＢＣＤ
ＡＢ、ＡＣ、ＡＤ、ＢＣ、ＢＤ、ＣＤ
Ａ、Ｂ、Ｃ、Ｄ
の１５通りです。
最初のＡＢＣＤの４つ以外の場合を省けば良いわけです。
（１）の第２項で使われる箱は
4Ｃ3で選ぶ箱が
| (1)ＡＢＣのときは | (2)ＡＢＤのときは | (3)ＡＣＤのときは | (4)ＢＣＤのときは
|
|---|
| ＡＢ、ＡＣ、ＢＣ | ＡＢ、ＡＤ、ＢＤ | ＡＣ、ＡＤ、ＣＤ | ＢＤ、ＢＤ、ＣＤ
|
| Ａ、Ｂ、Ｃ | Ａ、Ｂ、Ｄ | Ａ、Ｃ、Ｄ | Ｂ、Ｃ、Ｄ
|
（１）の第３項で使われる箱は
4Ｃ2で選ぶ箱が
| (1)ＡＢのときは | (2)ＡＣのときは | (3)ＡＤのときは | (4)ＢＣのときは
|
|---|
| Ａ、Ｂ | Ａ、Ｃ | Ａ、Ｄ | Ｂ、Ｃ
|
（１）の第４項で使われる箱は
4Ｃ1で選ぶ箱は
第１項ではどれも１回しか現れませんが、第２項や第３項では複数回現れます。
| | ＡＢＣ | ＡＢＤ | ＡＣＤ | ＢＣＤ
|
|---|
| 第２項 | １回 | １回 | １回 | １回
|
|---|
| 第３項 | - | - | - | -
|
|---|
| 第４項 | - | - | - | -
|
|---|
| | ＡＢ | ＡＣ | ＡＤ | ＢＣ | ＢＤ | ＣＤ
|
|---|
| 第２項 | ２回 | ２回 | ２回 | ２回 | ２回 | ２回
|
|---|
| 第３項 | １回 | １回 | １回 | １回 | １回 | １回
|
|---|
| 第４項 | - | - | - | - | - | -
|
|---|
| | Ａ | Ｂ | Ｃ | Ｄ
|
|---|
| 第２項 | ３回 | ３回 | ３回 | ３回
|
|---|
| 第３項 | ３回 | ３回 | ３回 | ３回
|
|---|
| 第４項 | １回 | １回 | １回 | １回
|
|---|
問題５
（２）のｍを６、ｎを５にして
