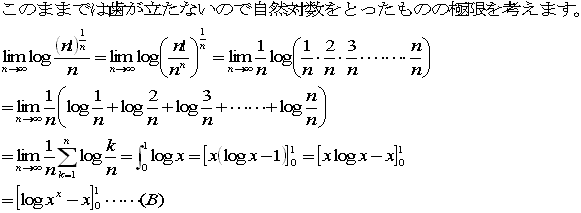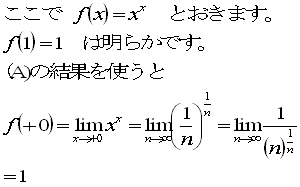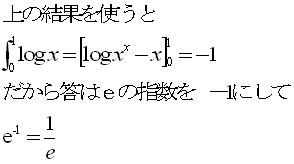NO.1684 分配問題 2007.8.15 水の流れ
先日生徒から、次のような分配問題の質問を受けました。一般の場合まで考えて作問をしました。
問題1:
1から5までの番号のついた5個のボールを、A,Bの2つの箱に、
どの箱にも少なくとも1個のボールが入るように入れる入れ方は何通りあるか。
問題2:
1から5までの番号のついた5個のボールを、A,B,Cの3つの箱に、
どの箱にも少なくとも1個のボールが入るように入れる入れ方は何通りあるか。
問題3:
1から5までの番号のついた5個のボールを、A,B,C,Dの4つの箱に、
どの箱にも少なくとも1個のボールが入るように入れる入れ方は何通りあるか。
問題4:
一般に、異なるm個のボールを、異なるn個の箱に、
どの箱にも少なくとも1個のボールが入るように入れる入れ方は何通りあるかを、
包除の原理を用いて、m、nと和の記号シグマを用いて表せ。ただし、m≧nとする。
問題5:
問題4で得た式を用いて、1から6までの番号のついた6個のボールを、
A,B,C,D,Eの5つの箱に、どの箱にも少なくとも1個のボールが入るように入れる入れ方は何通りあるか。
注:この記事に関する投稿の掲載は、2007年9月3日以降とします。
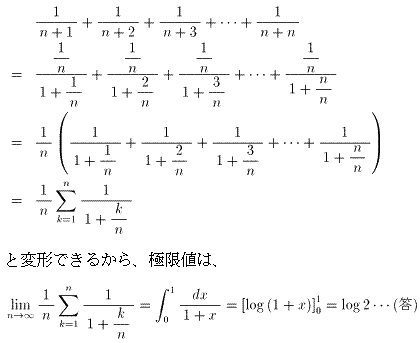
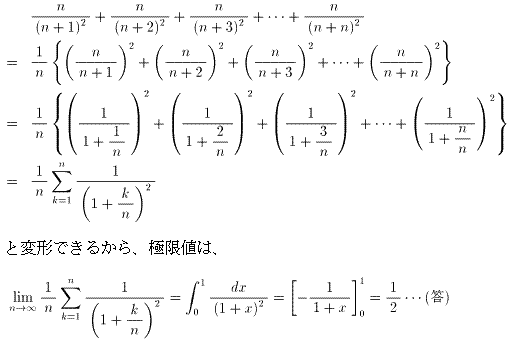
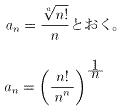
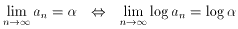
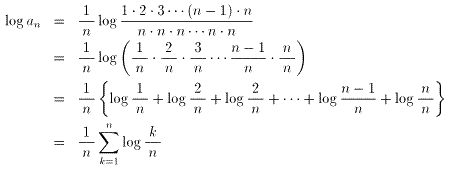
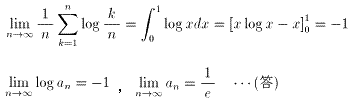
 (自然数nが大きいとき)
(自然数nが大きいとき)