NO.1681 極限値と定積分 2007.7.23 水の流れ
第１９４回数学的な応募問題
皆さん、微分積分学を学んでいくと、綺麗で美しいなーと思える公式に出会います。
太郎さんは 大学入試問題で極限値を求めるときに、下の公式を利用します。
＜出典：(1)、(2)は2006年芝浦工業大学（工学）(3)は日本数学検定協会監修の1級の問題集から＞
注：この記事に関する投稿の掲載は、２００７年８月１３日以降とします。
NO.1680 三角形の面積(2) 2007.7.23 夜ふかしのつらいおじさん
問題１
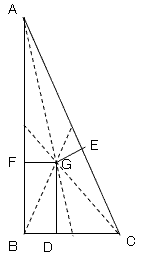
右の図で点線は中線です。
GD＝ｋ、GE＝ｍ、GF＝ｎは重心からの垂線です。
BC=ａ、ＣＡ＝ｂ、ＡＢ＝ｃとします。
△ＡＢＣの面積をＳとします。
Gが重心なので、中線が頂点の方から２：１に内分されているので、
△GBC＝△GCA＝△GAB（＝Ｓ／３）です。すると、ａｋ＝ｂｍ＝ｃｎ（＝２／３ Ｓ）です。
この値をｐとおくと
ａ＝ｐ／ｋ、ｂ＝ｐ／ｍ、ｃ＝ｐ／ｎ ・・・ （１）
です。
ヘロンの公式
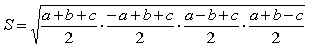
より、
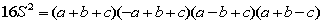
これに（１）を代入し整理します。
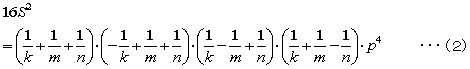
一方
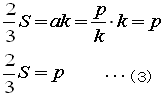
（２）、（３）を連立させて
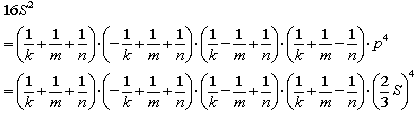
整理して
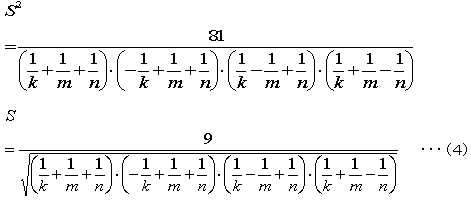
ここでｋ＝4、ｍ＝5／3、ｎ＝20／13を代入すると、Ｓ＝３０
問題２
上の（４）が答です。
NO.1679 三角形の面積 2007.7.2 水の流れ
第１９３回数学的な応募問題
先日、大学時代の数学科の仲間に会う機会がありました。その中で次のような問題を紹介されました。
でも、答えまでの言及はありません。皆さん！考えてください。
三角形ＡＢＣがあり、その重心をＧとする。Ｇから辺ＢＣ，ＣＡ、ＡＢまでの垂線の長さをそれぞれ
ｋ、ｍ、ｎとするとき、次の問題を解いてください。
問題１：ｋ＝４，ｍ＝５／３，ｎ＝２０／１３のとき、三角形ＡＢＣの面積を求めよ。
問題２：三角形ＡＢＣの面積をｋ、ｍ、ｎで表してください。
注：この記事に関する投稿の掲載は、２００７年７月２３日以降とします。
NO.1678 勝敗の差(2) 2007.7.2 夜ふかしのつらいおじさん
問題１
考えやすいように、勝つ確率をｐ、負ける確率をｑとします。
ただし、ｐもｑも1/2で同じ値です。
すると勝敗の差の期待値Ｅ2n-1は、
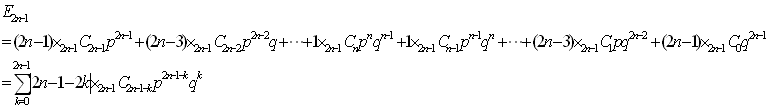
ここで、ｐ+ｑ（＝１）を掛けます。
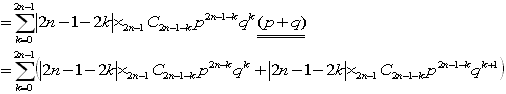
ここで、ｐとｑの積は次数が同じならすべて等しいので
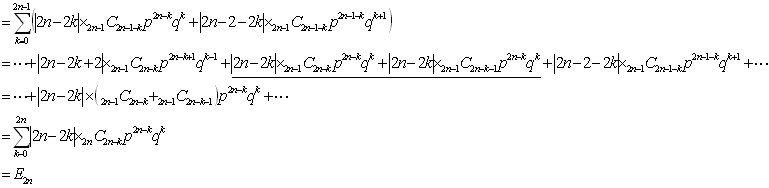
となり示されました。
下から４行目は、ｋ-1番目とｋ番目の式を並べています。
ちょっと分かりづらいので具体的にＥ3で書いてみます。
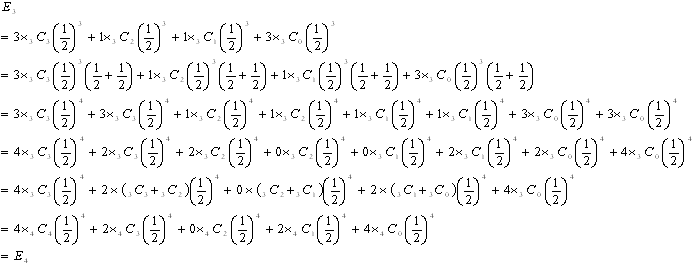
問題２
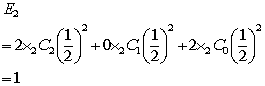
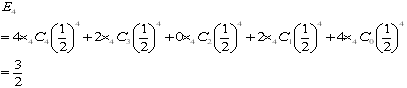
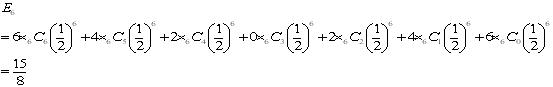
問題３
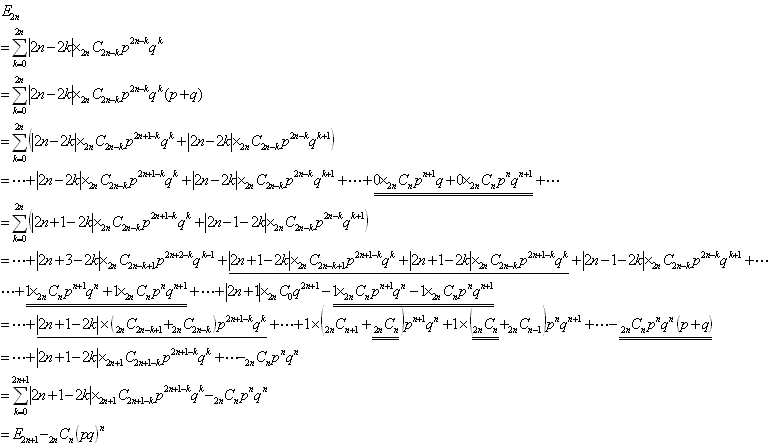
つまり
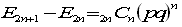
ｎを１下げて
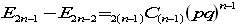
この式について、ｎを2からｎまで変えると
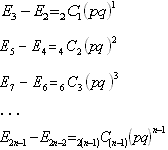
これらの式をＥ2k-1＝Ｅ2kに注意して加えると
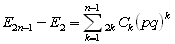
ここで、Ｅ2＝１、Ｅ2n-1＝Ｅ2nに注意すると
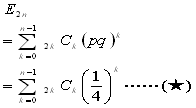
問題４
ウォーリスの公式を、
ｎ→∞のとき、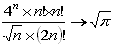
とすると、変形して
ｎ→∞のとき、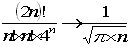
この式の左辺は、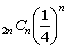
だからｎが大きいときには、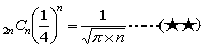
（★）の式がまとまれば良いのですが、どうもうまくいきません。
そこで、ｎ＝３までは問題２の解答を用い、ｎ＝４以降は（★★）の式を用いて エクセルで計算するとだいたい、
9.30355・・・
となります。
