NO.1633 ４つの町を訪問 2006.12.25. 真夏のサンタ
次の問題に関して疑問を持っています。
ある人がA、B、C、Dの4つの町を訪ねます。この人は忘れっぽく、
1度行った町のことはすぐに忘れます。
そのためある町から次にどの町に移動するかは常に3分の1の確率です。
この人が全ての町に行くには何回移動すればよいでしょうか？平均をもとめてください。
NO.1632 自然数の分割 2006.12.25 水の流れ
第１８４回数学的な応募問題
自然数ｎをいくつかの自然数の和として、
ｎ＝ｎ１＋ｎ２＋・・・＋ｎｒ（ｒ≧１）
の形に表すことを考える。この分割の総数をＱ（ｎ）とする。
例えばｎ＝３のとき、１＋１＋１、１＋２、２＋１、３ の４通りに表されるから、Ｑ（３）＝４となる。
次に、項の順序を考えた
１≦ｎ１≦ｎ２≦・・・≦ｎｒ のときの総数をＰ（ｎ）とする。
例えばｎ＝３のとき、１＋１＋１，１＋２，３の３通りになるからＰ（３）＝３となる。
さらに、ここで、ｎをこのような和で表すすべての表し方について、
項の積
ｎ１×ｎ２×・・・×ｎｒ
を考え、その最大値をＭ(ｎ) とする。
例えばｎ＝３のとき、項の積は１×１×１＝１，１×２＝２，３となるから、Ｍ（３）＝３となる。
ここから、問題です。
問題１：Ｑ(ｎ）を求めよ。
最初に、ｎ＝１，２，３，４，５，６と具体的に求めてから、考えてください。
答えは指数の形でも良い。
問題２：Ｐ(ｎ)をｎで表したいのですが、未解決問題でして、
そこで、ｎ＝１，２，３，４，５，６、７，８，と具体的に求めてから、
ｎ＝20までのＰ(ｎ)を知りたい。ここは、オイラーの５角数定理を用いて、
次の漸化式を利用してください。
Ｐ(ｎ)＝Ｐ(ｎ―１)＋Ｐ(ｎ―２)―Ｐ(ｎ―５)―Ｐ(ｎ―７)＋Ｐ(ｎ―１２)＋Ｐ(ｎ―１５)―Ｐ(ｎ―２２)―Ｐ(ｎ―２６)＋・・・
ただし、Ｐ(０)＝１とする
問題３：Ｍ(ｎ)を求めよ。
最初に、ｎ＝１，２，３，４，５，６、７、８と具体的に求めてから、考えてください。
注：この記事に関する投稿の掲載は、２００７年１月１５日以降とします。
NO.1631 最高位の数字(2) 2006.12.25. 夜ふかしのつらいおじさん
この問題は数学的に解いたというわけではありません。
エクセルで数えた個数
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 計
|
|---|
| 個数 | 167 | 99 | 68 | 54 | 45 | 37 | 31 | 30 | 24 | 555
|
|---|
無限個のときからの予想
| Ｎ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 計
|
|---|
| 常用対数 | 0.0000 | 0.4010 | 0.4771 | 0.6021 | 0.6990 | 0.7782 | 0.8451 | 0.9031 | 0.9542 | 1.0000 | −
|
|---|
| "先頭の数字がＮの確率" | 0.4010 | 0.1761 | 0.1249 | 0.0969 | 0.0792 | 0.0669 | 0.0580 | 0.0512 | 0.0458 | − | 1.0000
|
|---|
| "555個のときの予想" | 167.1 | 97.7 | 69.3 | 53.8 | 43.9 | 37.2 | 32.2 | 28.4 | 25.4 | − | 555
|
|---|
先頭の数字Ｎが４ということは、
４×１０k≦ ２n ＜ ５×１０k
となる整数ｋがあるということです。
常用対数をとると、log（５）＝log（１０／２）＝１−log（２）なので
ｋ＋２log（２） ≦ ｎlog（２） ＜ （ｋ＋１）−log（２）
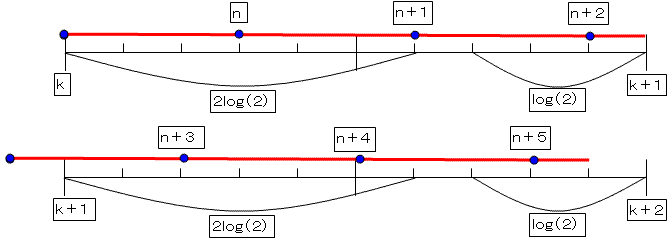
この図は、ｋ＝０で、ｎ＝１のときの様子を表しています。
右に書ききれないので下につなげています。
青の点は間隔がlog（２）で、黄色いゾーンは間隔が１ごとに現れます。
図の黄色いところに、青の点が入れば、先頭の数字が４ということになります。
間隔が有理数と無理数なので、周期のある関係にはなりえません。
先頭の数字がＮということは、
N×１０k ≦ ２n ＜ （Ｎ＋１）×１０k
となる整数ｋがあるということです。
常用対数をとると、
ｋ＋log（Ｎ） ≦ ｎlog（２） ＜ ｋ＋log（Ｎ＋１）
となるので、ｋから（ｋ＋１）の幅１の範囲で、先頭の数字がＮとなるゾーンは、
ｌｏｇ（Ｎ＋１）−ｌｏｇ（Ｎ）＝ｌｏｇ（１＋１／ｎ）
の幅があるということになります。
NO.1630 朝日新聞「ニッポン人脈記」 2006.12.16. Junko
朝日新聞の夕刊に連載されている「ニッポン人脈記」
では、12月11日(月曜日)から、〈数学するヒトビト〉 がテーマになっています。
第１回目は、ゼータ関数や、加藤和也氏作「素数の歌」なども登場します。
第４回では、雑誌「大学への数学」がテーマになっています。来週の記事も楽しみです。
NO.1629 最高位の数字(1) 2006.12.4. 水の流れ
第１８３回数学的な応募問題
皆さん、今年度早稲田大学（教育学部）の入試問題を参考して出題します。是非チャレンジください。
２５５５は十進法で表すと１６８桁の数で、その最高位（先頭）の数字は１である。
集合｛２ｎ｜ｎは整数で１≦ｎ≦５５５｝の中に、十進法で表した最高位の数字Ｎについて、
問題：Ｎ＝４は何回現れるか。
追加問題、Ｎ＝１，２，３，５，６，７，８，９はそれぞれ何回現れるか気になります。誰か教えてください。
注：この記事に関する投稿の掲載は、１２月２５日以降とします。
