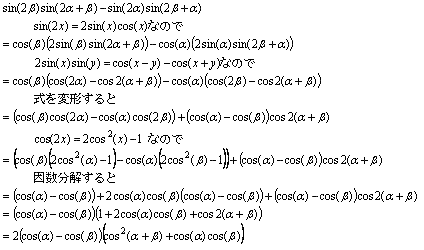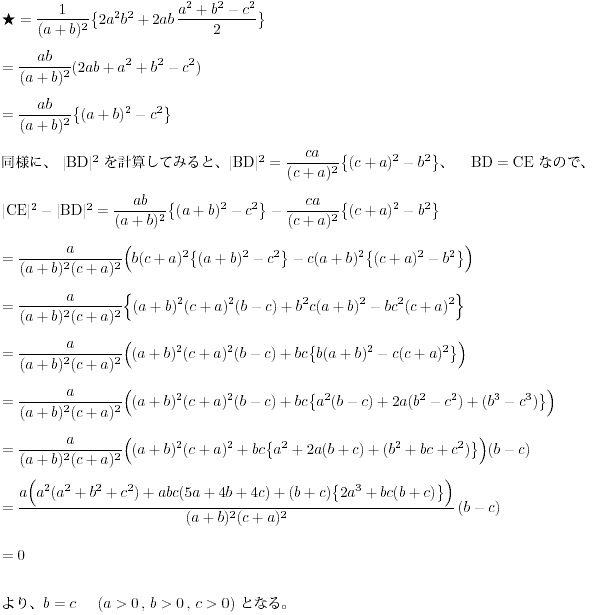ColloquiumNO.209
|
皆さん、日常生活の出来事で完全順列という考え方はよくあります。
１からｎまでの番号のついている箱と球があって、１つの箱に１個の球を入れていきます。
箱の番号と球の番号がすべて異なるような場合の数を数列｛ａｎ｝とするとき、次の問に答えよ。
問１：数列｛ａｎ｝の初項から第４項まで求めてください。
問２：ａｎをn ，ａｎ−１，ａｎ−２を用いて関係式を求めてください。
問３：数列｛ａｎ―ｎａｎ−１｝の一般項をｎで求めてください。
問４：箱の番号と球の番号がすべて異なる確率をPｎとする。
ｎ→∞のとき、Pｎの極限値求めてください。
注：この記事に関する投稿の掲載は、１０月１日以降とします。
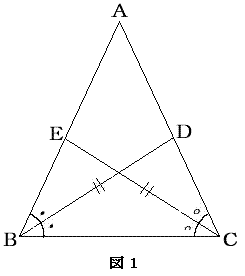
二等辺三角形の左右対称性を利用すれば、計算抜きでできそうな気がしたので、やってみました。
右図の線分BD，CEの長さは、辺BCの長さが一定とすれば、角ＢとＣで決まります。
そこで例えば、BDの長さを関数f(Ｂ，Ｃ)で表します。
f(Ｃ，Ｂ)は明らかに、CEの長さです。証明すべきことは、
f(B,C)=f(C,B)→B=C
です。
［証明］
f(Ｂ，Ｃ)＝f(Ｃ，Ｂ)＝rとします。
f(Ｂ，Ｃ)を3次元空間内の2次元の曲面グラフと考えて、
rの等高線に注目します。それがどんな形かは知りませんが、
それが、図-1の太実線のようだったとします。
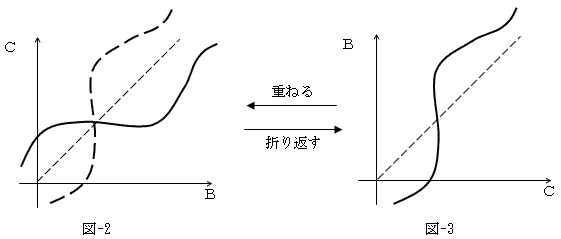
一方、f(Ｃ，Ｂ)＝rの等高線は、図-2のＢ軸とＣ軸を入れ換えたものなので、
図-2の太実線を、原点を通る45°の直線Ｂ＝Ｃで折り返した形になります（図-3）。
ところでいずれの等高線も、少なくともＢまたはＣの関数です。
従って、図-3の曲線を、図-2の同じ位置に重ねた場合（図-2の太破線）、
太実線と太破線は、互いに互いの逆関数になります。太実線と太破線の交点は、
Ｂ＝Ｃ上にしかないことを示します。
そのために、太実線の概形を描きます。図-4では、図-1の二等辺三角形の状態から、
CEの長さを変えずに角Ｂ，Ｃを変化させたらどうなるか、やってみました。
ケースは図-4-1と4-2の二つに大別できます。
まず図-4-1の場合ですが、図-1の△BCEが潰れた状態α点から始め、
β，γ，δの順番で、△BCEを膨らませていきます。δ点では、角Ｃ＝πとなり、
そこで終わりです。このとき(Ｂ，Ｃ)の挙動は以下となります。
α点 ： Ｂ＝Ｃ＝0
α→β： Ｂ単調増加，Ｃ単調増加
β点 ： このとき△ABCは二等辺三角形で、Ｂ＝Ｃ
β→γ： Ｂ単調増加，Ｃ単調増加
γ点 ： Ｂ最大
γ→δ： Ｂ単調減少，Ｃ単調増加
δ点 ： Ｃ＝πで最大
以上の挙動を図示すると、図-5となります。
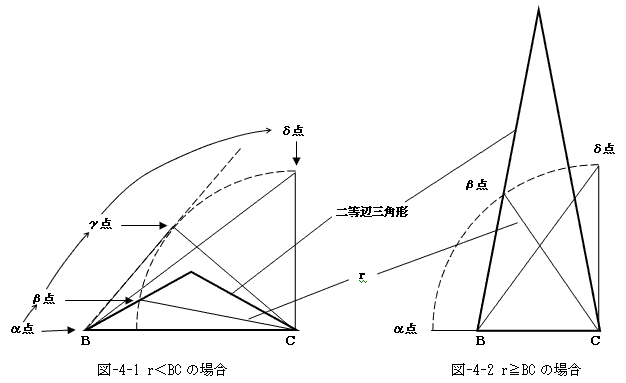
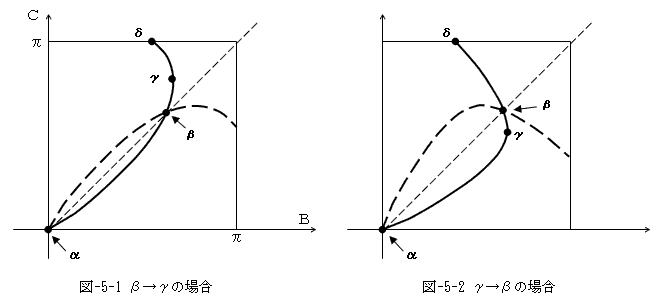
図-5-1は、図-4-1そのままの状態です。図-5-2は、図-4-1にようにr＜BCであっても、
β点とγ点の順序が前後するケースもあるので考慮しましたが、本質的な差はありません。
△BCEが潰れた状態(Ｂ，Ｃ)＝(0，0)を除けば、Ｂ＝Ｃ以外で、
f(Ｂ，Ｃ)＝f(Ｃ，Ｂ)＝rを満たす点はありません。次に図-4-2の場合ですが、
こっちはもっと簡単で、ＢとＣはいつでも単調増加か単調減少です。ただし、
r＞BC： Ｂ＝π から単調減少，Ｃ＝0から単調増加
r＝BC： Ｂ＝π/2から単調減少，Ｃ＝0から単調増加
という2つのケースに分かれます。これらを図-6に示しますが、やはり本質的な差はありません。
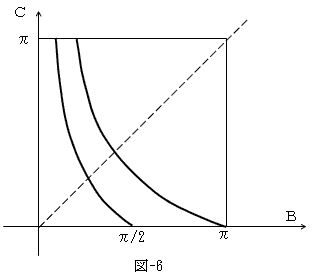
図-5-1，図-5-2，図-6より、△BCEが潰れた状態(Ｂ，Ｃ)＝(0，0)を除けば、
f(Ｂ，Ｃ)＝f(Ｃ，Ｂ)＝rは、Ｂ＝Ｃのみで満たされる。
［証明終］
ところで、以上の証明は、大幅な簡略化が可能です。 それは図-4-1と4-2が書けた時点で、Ｃは単調増加とわかるので、 この一言で、(0，0)を除けば、互いに互いの逆関数であるf(Ｂ，Ｃ)＝rとf(Ｃ，Ｂ)＝rの交点は、 Ｂ＝Ｃ以外にないことがいえます。つまりrの等高線は巻かないので、自分やその対称図形とぶつかる事はないわけです（図を書いてみて、やっと気づきました）。 ところがそうすると、今度はf(Ｂ，Ｃ)＝rの等高線の存在をいう必要がありますが、 rとしてr＝f(Ｂ，Ｂ)をとり、rを変えないように左右対称にr＝f(Ｂ，Ｃ)＝f(Ｃ，Ｂ)を 作図できる事は明らかですから、これで終わりです。
