NO.1606 二等辺三角形? 2006.8.21. 水の流れ
皆さん、平面幾何の問題で、一見簡単そうで解きづらいことがありませんか。
この問題がいい例になります。チャレンジください。
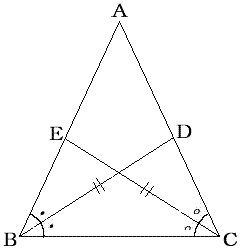
三角形の二つの角のそれぞれの二等分線を引き、それぞれの線が対辺に交わる点までの長さが等しいとする。
(図のBD=CE)
このとき、この三角形は二等辺三角形であることを証明してください。
注:この記事に関する投稿の掲載は、9月11日以降とします。
ColloquiumNO.208
|

皆さん、平面幾何の問題で、一見簡単そうで解きづらいことがありませんか。
この問題がいい例になります。チャレンジください。
三角形の二つの角のそれぞれの二等分線を引き、それぞれの線が対辺に交わる点までの長さが等しいとする。
(図のBD=CE)
このとき、この三角形は二等辺三角形であることを証明してください。
注:この記事に関する投稿の掲載は、9月11日以降とします。
先日、興味深い、発散する無限級数について証明しましたので、お知らせします。
一辺rの正方形を、右方向に無限につなげた図形(fig.1)を考える。
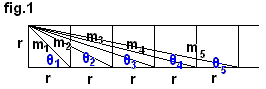
この時、m1、m2、・・・、mk および
sinθ1、sinθ2、・・・、sinθkの値は、table1のようになる。
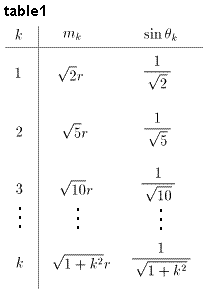
0<θk<π/2であるから、あきらかに全てのθkについて、
sinθk<θk<tanθk (k=1、2、3・・・)
である。よって、
sinθ1+sinθ2+sinθ3+・・・<θ1+θ2+θ3+・・
table1 およびfig.2、式1より式2が成り立つ。
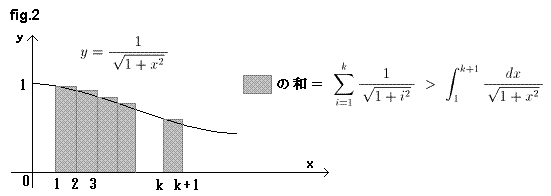
式1.
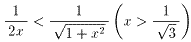
式2.
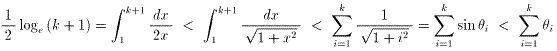
故に、
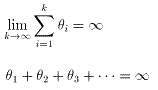
皆さん、賭け事のゲームをしていて、いつやめるかの引き際を考えたことはありませんか。
『A』 ここに、目が自然数の1から6までの正6面体のサイコロがあります。
問題1:正6面体のサイコロを1回または2回振り、最後に出た目の数を得点とするゲームを考える。 1回振って出た目を見たうえで2回目を振るか否かを決めるのである。どのように引き際を判断すると良いか。
問題2:上と同様のゲームを3回振ることが可能なら、2回目、3回目を振るか否かの決定は、 どのようにするに引き際を判断すると有利か。また、このゲームで得点の100倍のお金がもらえるとき、 掛け金400円を払って挑戦するのは得か損か。
さて、『B』今度は目が自然数の1から20までの正二十面体のサイコロに変えます。
問題3:正20面体サイコロを1回または2回振り、最後に出た目の数を得点とするゲームを考える。 1回振って出た目を見たうえで2回目を振るか否かを決めるのである。どのように引き際を判断すると良いか。
問題4:上と同様のゲームを3回振ることが可能なら、2回目、3回目を振るか否かの決定は、 どのように引き際を判断すると良いか。
問題5:さらに、上と同様のゲームを5回振ることが可能なら、2回目、3回目、4回目、5回目を振るか否かの決定は、 どのように引き際を判断すると良いか。 また、このゲームに得点の100倍のお金がもらえるとき、掛け金1500円を払って挑戦するのは得か損か。
注:この記事に関する投稿の掲載は、8月21日以降とします。
