| NO.1601 | 2006.6.25. | まこぴ〜 | 平方数の和と差(5) |
副題:「平方数の和と差」から「平方数の和」へ・・・そして・・・
例によって
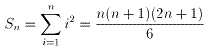
とします。
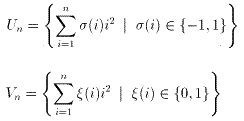
V’n={x|x:整数、0≦x≦Sn}−Vn
という3つの集合族{Un},{Vn},{V’n}を考えます。
言葉で言い表すと、次のような感じでしょうか:
Un:「長さnの式」の集合。
Vn:「n以下の自然数の平方数の和」の集合。
V’n:「『n以下の自然数の平方数の和』の形で表現できない、Sn以下の自然数」の集合。
そこで、
ξ(i)=0 のとき σ(i)=−1
ξ(i)=1 のとき σ(i)=1
という対応のもとにUnとVnは「式」のベースで一致し、さらにこの対応から
fn(x)=(x+Sn)/2
で、UnとVnに「値」としての1対1対応を与えることができます。
つまり、「平方数の和と差」を考えることが「平方数の和」を考えることに置き換わります。
{Vn}{V’n}を「値」で書き出してみます。
V0={0}
V1={0,1}
V2={0,1,4,5}
V3={0,1,4,5,9,10,13,14}
V4={0,1,4,5,9,10,13,14,16,17,20,21,25,26,29,30}
V5={0,1,4,5,9,10,13,14,16,17,20,21,25,26,29,30,34,35,38,39,41,42,45,46,50,51,54,55}
V6={0,1,4,5,9,10,13,14,16,17,20,21,25,26,29,30,34,35,36,37,38,39,40,41,42,45,46,49,50,51,52,53,54,55,56,57,61,62,65,66,70,71,74,75,77,78,81,82,86,87,90,91}
V’0={} (空集合)
V’1={}
V’2={2,3}
V’3={2,3,6,7,8,11,12}
V’4={2,3,6,7,8,11,12,15,18,19,22,23,24,27,28}
V’5={2,3,6,7,8,11,12,15,18,19,22,23,24,27,28,31,32,33,36,37,40,43,44,47,48,49,52,53}
V’6={2,3,6,7,8,11,12,15,18,19,22,23,24,27,28,31,32,33,43,44,47,48,58,59,60,63,64,67,68,69,72,73,76,79,80,83,84,85,88,89}
となります。Vn、V’nについて
1. Vn⊂Vn+1
2. P∈Vn ならば Sn−P∈Vn
3. P∈V’n ならば Sn−P∈V’n
が成り立ちます。
(証明)
P∈Vnとすると、ξ(i)∈{0、1}によって
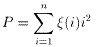
と表すことができる。
1.
ξ’(i)=ξ(i) (1≦i≦n)
=0 (i=n+1)
とすると、ξ’(i)∈{0、1}で
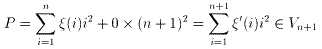
2.
ξ’(i)=1−ξ(i)
とすると、ξ’(i)∈{0、1}で
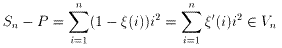
3.
2.の対偶である。(証明終わり)
Vnを、強引に表現するとすれば、
Vn=Vnー1∪(Vnー1+n2)
となります。ただし、加法「+」が定義できる集合Aがあり、b∈A、B⊂Aにたいして、
B+b={x+b|x∈B}
とおきます。
V’nの元の個数を観察して、驚きました。(プログラムにて検証)
注)#(A)は、集合Aの元の個数を表します。
#V’0= 0
#V’1= 0
#V’2= 2
#V’3= 7
#V’4= 15
#V’5= 28
#V’6= 40
#V’7= 52
#V’8= 58
#V’9= 62
#V’10= 62
#V’11= 62
#V’12= 62
n≧9であれば、どうやら#V’n= 62 となる「らしい」。
さらに、上述の2.3.により
4.Vn,V’nの分布はSn/2を中心に対称な配置となる。
ついでに、V’nの「前半の31個」は、n>9であれば
X={2, 3, 6, 7, 8, 11, 12, 15, 18, 19, 22, 23, 24, 27, 28, 31, 32, 33, 43, 44, 47, 48, 60, 67, 72, 76, 92, 96, 108, 112, 128}
で固定されている(プログラムで計算)。この31個は、平方数の和との形に表現できない自然数です。
では、
問題:「平方数の和とはならない数」が、この31個だけか?
が次の課題となる。上に挙げた31個は、プログラムではじきだしただけであるので、証明には、程遠い。
これが、解決できれば、議論を逆にたどることで、大元の「長さnの式」Unを全て求めることになる。
挑戦は続く・・・・

 E-mail
E-mail
 戻る
戻る