| NO.1567 | 2006.1.1 | Junko | 怴擭偁偗傑偟偰偍傔偱偲偆偛偞偄傑偡丅 |
2006擭丄偁偗傑偟偰偍傔偱偲偆偛偞偄傑偡丅
嶐擭偼丄偮偔偽偱偺侾儢寧偵搉傞尋廋丄俀嶜栚偺杮偺弌斉側偳丄
懡偔偺恖偵巟偊傜傟偰條乆側偙偲偵庢傝慻傓偙偲偑偱偒偨偲怱偐傜姶幱偟偰偍傝傑偡丅
崱擭傕帺暘偺抲偐傟偨応偱丄慡椡傪恠偔偟偰偄偗傞傛偆寬峃偵棷堄偟偰偑傫偽傝偨偄偲巚偄傑偡丅
杮擭傕偳偆偧傛傠偟偔偍婅偄偄偨偟傑偡丅

| NO.1568 | 2006.1.10. | 栭傆偐偟偺偮傜偄偍偠偝傫 | 惣楋俀侽侽俇擭乮俀乯 |
栤戣侾丗彫挰嶼
丂挧愴偟傑偣傫偱偟偨丅
栤戣俀丗Four Fourth 栤戣
丂挧愴偟傑偣傫偱偟偨丅
栤戣俁丗侾楢懕偡傞婔偮偐偺帺慠悢偺榓
2006偑(k+1)屄偺帺慠悢偺榓偲偟傑偡丅
嵟弶偺悢傪値偲偡傞偲丄弴偵値丆(n+1)丆(n+2)丆丒丒丒丆(n+k)偺榓偵側傝傑偡丅
1+2+3+丒丒丒+k亖k(k+1)乛2丂側偺偱
丂丂丂(2006亅k(k+1)乛2)乛(k+1)亖値
偙傟傪惍棟偡傞偲丄
丂丂丂4012亖(k+1)(k+2n)
傑偨丄4012亖2亊2亊17亊59側偺偱(k+1)偲偟偰4012偺栺悢傪摉偰偼傔偰傒傞偲丄
| (1) | 侾屄偺偲偒丄 | 2006 |
| (2) | 係屄偺偲偒丄 | 500亄501亄502亄503 |
| (3) | 侾俈屄偺偲偒丄 | 110亄111亄112亄丒丒丒亄126 |
| (4) | 俆俋屄偺偲偒丄 | 5亄6亄7亄丒丒丒亄63 |
栤戣係丗俁屄偺嶰妏悢偺榓
偙傟偼偨偔偝傫偺夝偑偁傝傑偡丅乮16屄乯
n(n+1)乛俀偺n偺慻傒崌傢偣傪彂偔偲丄
| (1) | 侾丆俁侽丆俆俆 | (9) | 侾係丆係侽丆係俇 |
| (2) | 侾丆俁俋丆係俋 | (10) | 侾俇丆俁係丆俆侽 |
| (3) | 係丆侾係丆俇侾 | (11) | 侾俋丆俀俁丆俆俆 |
| (4) | 係丆係侽丆係俉 | (12) | 俀俀丆俁俀丆係俋 |
| (5) | 俈丆俀俆丆俆俈 | (13) | 俀俆丆俀俉丆俆侽 |
| (6) | 俈丆俁俈丆俆侽 | (14) | 俀俆丆係侽丆係侾 |
| (7) | 侾俀丆俁俈丆係俋 | (15) | 俀俉丆俁俋丆係侽 |
| (8) | 侾係丆侾俋丆俆俉 | (16) | 俁侽丆俁係丆係俁 |
栤戣俆丗係屄偺巐妏悢偺榓
偙傟偼栤戣係傛傝傕偭偲偨偔偝傫偺慻傒崌傢偣偑偁傝傑偡丅
値2偺値偺慻傒崌傢偣傪彂偔偲丄
| (1) | 侾丆係丆侾俆丆係俀 | (7) | 侾丆俀俁丆俀係丆俁侽 |
| (2) | 侾丆係丆俁侽丆俁俁 | (8) | 俀丆俁丆侾俀丆係俁 |
| (3) | 侾丆俋丆侾俉丆係侽 | (9) | 俀丆俋丆俀侽丆俁俋 |
| (4) | 侾丆俋丆俁侽丆俁俀 | (10) | 俀丆俋丆俀俆丆俁俇 |
| (5) | 侾丆侾俀丆俁侽丆俁侾 | (11) | 俀丆侾俆丆侾俇丆俁俋 |
| (6) | 侾丆侾俆丆俀俀丆俁俇 | 丒丒丒 |
慻傒崌傢偣偼偙偺悢攞偼偁傝傑偡偑丄帪娫偺搒崌偱慡晹偼挷傋傑偣傫偱偟偨丅
仸丂栤戣係丄俆偼僄僋僙儖傪巊偭偰僀儞僠僉偱夝偒傑偟偨丅 椺偊偽栤戣俆偼廲墶偵暯曽悢傪暲傋丄廲墶偺僋儘僗偡傞偲偙傠偵俀偮偺暯曽悢偺 榓傪寁嶼偝偣傑偡丅俀侽侽俇偐傜偦偺悢傪堷偄偨悢偑昞偺拞偵偁傟偽儅乕僋傪晅 偗傞傛偆側僔乕僩傪嶌傝娤嶡傪偟偰傒傑偟偨丅
栤戣俇丗扨埵暘悢偺榓
偙傟偼丄俀侽侽俇亖俀亊侾俈亊俆俋偑僸儞僩偱偡丅
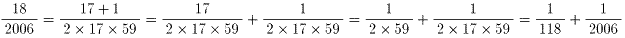

| NO.1569 | 2006.1.10. | 悈偺棳傟 | 暯柺婔壗 |
栤侾偺惵帤晹暘乮撪怱仺廳怱乯偺掶惓乮2006.1.26.)
栤侾偺愒帤晹暘乮撪怱仺廳怱乯偺掶惓乮2006.1.29.)
奆偝傫丄崱寧偺俀侾擔俀俀擔戝妛擖帋僙儞僞乕帋尡偑慡崙奺抧偱峴傢傟丄怴壽掱偺嵟弶偺惗搆偑庴尡惗偟傑偡丅
偦偺拞偱悢妛嘥丒俙偺壢栚偵乽暯柺婔壗乿偑偁傝傑偡丅
慜擔丄師偺傛偆側栤戣傪乽忋條乿偐傜庴偗庢傝傑偟偨丅夝偄偰傒偰偔偩偝偄丅
栤侾丗嶰妏宍ABC偺廳怱傪D偲偟偰偱偒傞嶰妏宍ABD
丄嶰妏宍DBC偺廳怱傪偦傟偧傟P,Q偲偟丄
AB=係丂BC=俉 妏B亖俋侽偲偟偨偲偒PQ偺挿偝傪丂夝偒曽傪揧偊偰摎偊傛丅
栤俀丗嶰妏宍ABC偺撪怱傪I偲偟丄妏A亖俇侽並丄捈慄CI偺墑挿偲AB偺岎揰傪E丄捈慄BI偺墑挿偲AC偺岎揰傪D偲偟偨帪
EI亖ID傪徹柧偣傛丅
栤俁乮擄乯丗嶰妏宍ABC偺撪怱傪I丂奜怱傪O丂奜愙墌偺敿宎傪R丂撪愙墌偺敿宎傪倰偲偟偨帪
丂丂丂俀R倰亖R2乗OI2
偵側傞偙偲傪徹柧偣傛丅
栤係乮桳柤丗墌偵撪愙偡傞惓嶰妏宍ABC偑偁傝屖BC乮偲傝偁偊偢抁偄傎偆偲愝掕偟傑偡乯忋偵
彑庤側揰P傪庢傞偲偒丄
丂丂丂PA亖PB+PC
偱偁傞偙偲傪擇捠傝偺徹柧傪偣傛丅
栤俆丗敿宎俀偺墌廃忋偵係揰ABCD傪屖AB丗屖BC丗屖CD丗屖DA亖係丗係丗俁丗侾偲側傞傛偆偵偲傞偲偒丄AD偺挿偝傪摎偊傛丅

| NO.1570 | 2006.1.12. | teki | 惣楋俀侽侽俇擭乮俁乯 |
栤戣侾偺彫挰嶼傪峫偊偰尒傑偟偨丅
丂丂丂俀侽侽俇亖乮侾亄乮俀亊俁亄係乯亊俆亄俇俈乯亊乮俉亄俋乯
偙傫側偺偱丄偄偄偺偱偟傚偆偐丠

| NO.1571 | 2006.1.14. | teki | 惣楋俀侽侽俇擭乮係乯 |
栤戣俀偺俥倧倳倰丂俥倧倳倰倲倛偱偡偑丄巐懃墘嶼婰崋偲妵屖丄彫悢揰丄弞娐彫悢丄傋偒忔
偩偗偱偼嬯偟偄傛偆偱偡丅
奼挘婰崋偲偟偰丄僈僂僗婰崋偐嚁婰崋偑巊偊傟偽壗偲偐側傝偦偆偱偡偑丒丒丒丅
椺偊偽丄嚁婰崋傪巊偭偨応崌丄偪傚偭偲嶌傝曽偼傑偢偄傫偱偡偑
丂丂丂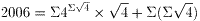
偱嶌傟傑偡丅
偨偩偟丄儼倠亖倠亄乮倠亅侾乯亄乮倠亅俀乯亄丒丒丒亄俀亄侾

| NO.1572 | 2006.1.15. | teki | 惣楋俀侽侽俇擭乮俆乯 |
栤戣俀偺俥倧倳倰丂俥倧倳倰倲倛偱僈僂僗婰崋傪巊偭偨傕偺丄堦墳偱偒傑偡偑丄偐側傝嬯偟偄偱偡丅
丂丂丂俀侽侽俇亖乵係亐丏丏丏係亊併係亊併併併併併併併併併併乮係両乯乶

| NO.1573 | 2006.1.19. | teki | 惣楋俀侽侽俇擭乮俇乯 |
偁傟偐傜丄壗偲偐嚁傗僈僂僗婰崋側偟偱偱偒側偄偐峫偊偰偄偨傫偱偡偑丄
偱偒傑偡偹丅
丂丂丂俀侽侽俇亖係亐併乮丏丏丏丏丏丏係乯亄係亄併係
係偑俀偮偱俀侽侽侽偑嶌傟偨傫偱偡偹丅

| NO.1574 | 2006.1.24. | 傑偙傄乣 | 係係係係偺栤戣(11) |
偝偰丄審柤偺乽侾侽侽乿偵娭偡傞夝偱偡偑丄係係側偳偺懡埵悢
傪擣傔傞側傜偽丄
丂丂丂侾侽侽亖係係亐丏係係
偲偄偆幃傕桳傝傑偡丅
嶲峫傑偱偵丄梀媃幒丂俹倃俶(Precedence of eXpression of Numbers)偲偄偆儁乕僕傪偛棗偔偩偝偄丅
傑偨丄PXN corporation
偲偄偆僒僀僩傕偁傝傑偡偺偱丄偺偧偄偰傒偰偔偩偝偄丅
| NO.1575 | 2006.1.24. | ohkubo | 乽嶼悢偲悢妛偺偩偄偛傒乿(3) |
堦岥偵乽悢妛乿偲尵偭偰傕丄偦偺拞恎偼偄偔偮偐偁傝傑偡丅戝偒偔暘椶偡傞偲丄嘆妛栤偲偟偰偺悢妛丄嘇摴嬶偲偟偰偺悢妛丄嘊恖娫幮夛偺儖乕儖偲偟偰偺悢妛乮偙傟偼嶼悢偐側乯丄嘋庴尡悢妛偲偄偭偨偲偙傠偱偟傚偆偐丅嵶暘壔偡傟偽傕偭偲偁傞偱偟傚偆偟丄傑偨丄偦傟傜傪尩枾偵掕媊偡傞偲尵偆偐丄柧妋側嫬奅傪愝偗傞偙偲偼側偐側偐擄偟偄傛偆偱偡丅偩偐傜偙偦乽悢妛乿偲堦妵傝偵偝傟偰偄傞傢偗偱偡偑丄偦偆偼尵偭偰傕丄傗偼傝堦偮堦偮偼偦偺惈幙傗懚嵼堄媊偼堘偆傕偺偱丄偦傟傜傪乽悢妛乿偲扨弮壔偡傞偙偲偵偼柍棟偑偁傝傑偡丅恖偵傕怓乆側僞僀僾偺恖偑偄傞偺偲摨偠偱偡丅偝偰丄偙偺拞偱丄擔杮偺悢妛嫵堢偱偼丄嘋偺庴尡悢妛偑戝偒側僂僄僀僩傪愯傔偰偄傑偡丅庴尡悢妛偼乽悢妛乿偲偟偰旕忢偵榗側柾條傪偟偰偍傝丄偦偺偨傔丄偄偄堄枴偱懆偊傜傟傞偙偲偼傑偢側偔丄愭惗偵傛偭偰偼丄庴尡悢妛偱側偄悢妛傕岅傠偆偲暠摤偟偰偄傞曽傕偄傜偭偟傖傞傛偆偱偡偑丄彮側偔偲傕崅峑傑偱偺抜奒偱乽悢妛乿偲屇偽傟偰偄傞傕偺偺幚懺偼愭惗偵傛偭偰掱搙偺嵎偙偦偁傟庴尡悢妛偱偡乮偦偆側傜偞傞傪摼側偄晹暘傕偁傞乯丅庴尡悢妛偑偳偆偄偆惈幙偺傕偺偱偁傞偐偼婛偵怓乆側曽偺尒夝偑帵偝傟偰偄傞偺偱徻偟偔怗傟傑偣傫偑丄偦偺榗偝備偊偵懡偔偺恖傪悢妛寵偄偵娮傟偰偄傞堦梫場偱偁傞偙偲偼娫堘偄側偄偙偲偱偟傚偆丅
偙偺偨傃弤巕愭惗偑挊偝傟偨杮偺僞僀僩儖偵偼乽嫵壢彂偲偼傂偲枴堘偆乿偲婰偝傟偰偄傑偡丅悢妛嫵堢偺尰忬偑庴尡悢妛偵孹幬偟偰偄傞偙偲偐傜偡傞偲丄戝孶嵕偐傕偟傟傑偣傫偑丄偙傟偼崱偺悢妛偺庡棳傪側偟偰偄傞庴尡悢妛傊偺挧愴忬偲夝庍偟偰傕偄偄偱偟傚偆丅妛峑帪戙丄庴尡悢妛偑岲偒偵側傟側偐偭偨巹偵偼丄偙偺僼儗乕僘偑偨偄傊傫儔僕僇儖偵塮傝丄傑偨偦偙偑婥偵擖傝傑偟偨丅摿偵丄悢妛偺愭惗帺恎偑偦偆偟偨僼儗乕僘傪宖偘偨偙偲偵戝偒側堄枴傪姶偠傞偲偄偆偐丄壗偐嫻偺偡偔巚偄偑偡傞偺偱偡丅偨傇傫丄堦晹偺悢妛偺愭惗曽偑彞偊傞僥儞僾儗乕僩壔偝傟偨悢妛傪妛傇堄媊偺庡挘偵偼傕偆暦偒朞偒偨偐傜偱偟傚偆丅
孞傝曉偟偵側傝傑偡偑丄擔杮偺悢妛嫵堢偺幚懺偼庴尡悢妛偱偡丅嫵壢彂傕庴尡嶲峫彂傎偳偱偼側偄偵偟偰傕偦偺斖醗偱偡丅偨偩丄偦偆側傞偺偼弌斉幮偺愑擟偲扨弮壔偡傞偙偲偼偱偒傑偣傫丅側偤側傜丄擖帋孹岦偐傜堩扙偟偨撪梕偱偼嵦戰偟偰傕傜偊側偄偐傜偱偡丅庴尡嶲峫彂偵偮偄偰傕帠忣偼帡偰偄傞偱偟傚偆丅偱偡偑丄堦斒彂偼偦傟偲摨偠偱偼僟儊偩偲巚偄傑偡丅堦斒偺悢妛彂愋偼庴尡悢妛偱偼姶偠傞偙偲偺偱偒側偄乬杮摉偺悢妛乭偺偍傕偟傠偝偺傛偆側傕偺傪揱偊傞撪梕偱偁偭偰偙偦弶傔偰弌斉偝傟偨抣懪偪偑偁傞偺偱偡丅庴尡悢妛偱乬杮摉偺悢妛乭偺偍傕偟傠偝傪尒幐偭偰偄傞恖偨偪偵丄乽悢妛偭偰丄杮摉偼偦偆偄偆傕偺偩偗偠傖側偄傛両乿偲帺怣傪帩偭偰慽偊傞偙偲偺偱偒傞傛偆側撪梕偱側偄偲乧丅偙偺偨傃弤巕愭惗偺彂偐傟偨杮偼丄僞僀僩儖偺捠傝嫵壢彂偺悢妛乮庴尡悢妛乯偲偼堘偆傕偺偱偁傝丄崱偺悢妛嫵堢偱悢妛寵偄偵側偭偰偟傑偭偨恖偨偪偵傕恊偟傔傞撪梕偱偡丅偲尵偆傛傝丄偦偆偄偆恖偨偪偵偙偦撉傫偱傎偟偄偲巚偄傑偡丅
偙偺杮偺嬶懱揑側挿強傪堦偮嫇偘傞偲丄婰弎偑懳榖宍幃偲側偭偰偄傞偙偲偱偡丅寴嬯偟偄暥懱偱堦曽揑偵乽偙偆側傞傫偩乿乽偙偆偡傟偽偄偄傫偩乿乽偙偆偟側偝偄乿側偳偲尵偄偨偘側撪梕偱偼寵偵側偭偰偟傑偄傑偡丅帪偵偼丄撉傫偱偄偰傓偐偮偄偰偔傞偙偲傕偁傝傑偡傛偹丅乽執偦偆偵乧乿偭偰偹丅弤巕愭惗偺杮偵偼偦偆偄偆強偑偁傝傑偣傫丅恖暱敳孮偺Junko愭惗偑惗搆乮偄偝偍孨乯偲懳榖偡傞拞偱丄惗搆乮偄偝偍孨乯偺媈栤偵堦偮堦偮挌擩偵暯堈側尵梩偱摎偊偰偄偔偲偄偆偐偨偪偵側偭偰偍傝丄悢妛寵偄偺恖偨偪偵傕偒偭偲撻愼傔傞傕偺偱偡丅嶶乆庴尡悢妛傪埆偔尵偭偰傞巹偱偡偑丄傓偐偟丄撪梕偼庴尡悢妛偱傕偄偄杮偑偁傝傑偟偨丅挿擭丄梊旛峑島巘傪偝傟偰偄偨搉曈師抝偝傫偺偲偄偆曽偺彂偐傟偨嶲峫彂偱偡丅偦偺嶲峫彂傕婰弎偑懳榖宍幃偩偭偨傫偱偡丅偦偺嶲峫彂偺偍偐偘偱丄偦傟傑偱戅孅偱偟傚偆偑側偐偭偨悢妛偺曌嫮乮偁偔傑偱庴尡悢妛偱偡偗偳乯偑嬯捝偱側偔側偭偨偺偱偡偑丄弤巕愭惗偺杮傪撉傫偱偄傞偲丄偦偺帪偺婰壇偑慼傝傑偡丅巹偼丄愭惗偲惗搆偺懳榖偱榖傪恑傔偰偄偔偲偄偆丄彮側偔偲傕摉帪偺悢妛嶲峫彂偲偟偰偼堎椺偺撪梕偵丄挊幰偺乽悢妛傪傢偐傜偣偨偄乿偲偄偆擬偄巚偄偲丄偦偺偨傔偺憂堄岺晇丄偦偟偰壗傛傝丄乽悢妛乮庴尡悢妛偱偁偭偰傕乯傪偱偒傞傛偆偵側傝偨偄乿偲婅偆妛惗傊偺廔巒堦娧偟偨桪偟偝傪姶偠偨傕偺偱偡丅媥宔僐乕僫乕偵偼彮偟偽偐傝揘妛揑側榖戣傕嵹偭偰偄傑偟偨偟丄偁偲偑偒偵偼丄庴尡悢妛偲乬杮摉偺悢妛乭偺堘偄傪堄幆偟偰偐丄乽庴尡偑廔傢偭偨傜偙偺杮偺撪梕偼朰傟偰傕傜偄偨偄乿偲偄偆偙偲傑偱彂偐傟偰偁傝丄乽偲偙偲傫妛惗巚偄偺恖偩側偁乿偲偄偆報徾偑巆傝傑偟偨丅偨偐偑庴尡悢妛偺愱栧壠側偺偐傕偟傟傑偣傫偑丄偦偺挊彂偐傜揱傢偭偰偔傞搉曈愭惗偺恖暱偺椙偝偼丄悢妛傪堄幆偡傞偙偲偺側偄擔忢傪憲偭偰偄傞崱偱傕朰傟傞偙偲偑偱偒傑偣傫丅巹偼丄偙偺偨傃弤巕愭惗偺彂偐傟偨杮偵傕丄壗偐搉曈愭惗偺杮偲帡偨傛偆側暤埻婥傪姶偠傞偺偱偡丅
乬恖暱乭偲偄偆尵梩偑弌偰偒偨偺偱嵟屻偵偪傚偭偲怗傟傑偡偑丄悢妛偑寵偄偵側傞庡側棟桼偵丄悢妛嫵巘偺恖暱乮恖奿乯傕嫇偘傜傟傑偡丅悢妛偵尷偭偨榖偱偼偁傝傑偣傫偑丄寵側恖暱乮恖奿乯偺嫵巘偵摉偨偭偰偟傑偭偨傜丄嫵傢偭偰偄傞偙偲帺懱偑寵偄側傞偺偼柍棟傕側偄偙偲偱偡丅偙傟偼偲偰傕巆擮側偙偲偱偡偑丄悢妛幰傪娷傔丄悢妛嫵巘偺拞偵偼堦晹恖暱乮恖奿乯偵栤戣偺偁傞恖偑懚嵼偟傑偡丅偦偺恖偨偪偼乽帺暘偼摿庩側嵥擻傪帩偭偰偄傞乿偲偱傕帺屓庡挘偟偨偄偺偐丄傓傗傒偵擄夝側尵梩傪巊偄丄恖傪尒壓傠偡傛偆側懺搙傪偲傝傑偡丅偱偡偑丄偦傫側攚怢傃偡傞傛偆側偙偲偼摉恖偺帺屓枮懌埲奜偺壗暔偱傕側偔丄妛傇懁偑媮傔偰偄傞偙偲偱偼偁傝傑偣傫偟丄偦傕偦傕悢妛偲偼墢傕備偐傝傕側偄傕偺偱偡丅偦傫側偙偲偵柌拞偵側偭偰偄傞嫵巘偵摉偨偭偰偟傑偭偨傜嵟埆偱偡丅嫵巘偺恖暱乮恖奿乯傕悢妛偺岲偒寵偄偵戝偒側塭嬁傪媦傏偟傑偡丅偟偐傕偦傟偼愭偵婰偟偨嘆乣嘋偺傛偆側悢妛偺撪梕埲慜偺栤戣偱偡偐傜丄偦偆偄偆偙偲傛傝傕偭偲傕偭偲廳梫側偙偲側偺偐傕偟傟傑偣傫丅悢妛傪岲偒偵側偭偰傕傜偆偵偼丄嫵巘帺恎偑尓嫊偵側偭偰偦傟傪妛傇懁偲摨偠栚慄偱峫偊偰偄偔偲偄偆巔惃偑昁梫偱偡丅悢妛傪岲偒偵側偭偰傕傜偆慜偵帺暘傪岲偒偵側偭偰傕傜偆偙偲偑戝愗側偺偱偟傚偆丅搉曈愭惗偲摨偠偔丄Junko愭惗偵傕偦傫側巔惃偑姶偠傜傟岲姶偑帩偰傑偡丅執傇偭偰偄傞寵側嫵巘偵摉偨偭偰偟傑偭偨偍偐偘偱悢妛偑寵偄偵側偭偨恖偨偪傕彮側偔側偄偱偟傚偆丅巹偼偦偆偄偆恖偨偪偵傕丄婥偝偔側恖暱偺Junko愭惗偲懳榖偟偰偄傞惗搆乮偄偝偍孨乯偵側偭偨偮傕傝偱偙偺杮傪撉傫偱傕傜偊偨傜偲巚偆偺偱偡丅悢妛偵懳偡傞僀儊乕僕偑曄傢傝傑偡丅偄傗丄乽崱傑偱帺暘偑寵偭偰偄偨偺偼幚偼悢妛偱偼側偔丄妛峑帪戙偺寵側悢妛嫵巘偩偭偨偺偩乿偲婥偯偔偲尵偭偨傎偆偑惓妋偱偟傚偆偐丅偲偵傕偐偔偵傕丄僟儊側偺偼乬寵側悢妛嫵巘乭偱偁偭偰悢妛偦偺傕偺偱偼偁傝傑偣傫丅悢妛偺枺椡偼幚偼斲掕偝傟偰偄側偄偺偱偡丅
巹偼丄偡偽傜偟偄愭惗偵弌夛偊傟偽丄悢妛偺枺椡偑偒偭偲尒偊偰偔傞偼偢偩偲巚偭偰偄傑偡丅偱偡偐傜丄孞傝曉偟偵側傝傑偡偑丄壗傜偐偺棟桼偱悢妛偺枺椡傪尒幐偭偰偄傞恖偨偪偵偙偦丄偙偺杮傪撉傫偱傕傜偊偨傜偲巚偄傑偡丅

| NO.1576 | 2006.1.29. | 悈偺棳傟 | 儁儖曽掱幃 |
愒帤晹暘偺掶惓乮2006.2.8.)
奆偝傫丄1998擭偺偍拑偺悈戝妛擖帋栤戣偐傜嶌栤偟傑偟偨丅僠儍儗儞僕偔偩偝偄丅
栤侾丗摍幃(倶俀亅俶倷俀)(倱俀亅俶倲俀)
亖(倶倱亄俶倷倲)俀乗俶(倶倲亄倷倱)俀丂傪徹柧偣傛丅
丂丂丂乮拲丗偙偺摍幃傪僽儔乕儅僌僾僞偺峆摍幃偲偄偆乯
丂儁儖曽掱幃偲偼俶傪暯曽幃偱側偄帺慠悢丄倣傪侽偱側偄惍悢偲偡傞偲偒丄
倶俀亅俶倷俀亖倣 偲偄偆宆偺晄掕曽掱幃傪偄偄傑偡丅偙偙偱丄曽掱幃倶俀亅俶倷俀亖倣 傪俹倣丂偲彂偔偙偲偵偟傑偡丅
(倶丆倷)偼俹倣 偺帺慠悢夝偱丄(倱丆倲)偼俹値 偺帺慠悢夝偱偁傞偲偡傞偲丄
栤侾偺塃曈偼儁儖曽掱幃偺宍傪偟偰偄傑偡丅嵍曈偼倣値偱偡偐傜丄(倶倱亄俶倷倲丆倶倲亄倷倱)偼儁儖曽掱幃俹倣値丂偺帺慠悢夝偱偡丅
丂椺偊偽丄倶俀亅俀倷俀亖乗俀偺帺慠悢夝偲
倱俀亅俀倲俀亖値偺帺慠悢夝偐傜丄俹乗俀値
丂偺帺慠悢夝(倶倱亄俀倷倲丆倶倲亄倷倱)傪嶌傝弌偡偙偲偑偱偒傑偡丅
偙偙偱丄俹乗俀偺帺慠悢夝(倶倠丆倷倠)偲俹侾偺帺慠悢夝(倱丆倲)偐傜
俹乗俀偺帺慠悢夝丂
丂(倶倠亄侾丆倷倠亄侾)
亖(倶倠倱亄俀倷倠倲丆倶倠倲亄倷倠倱)偑弌偰偒傑偡丅
偙偙偐傜栤戣偵偟傑偡丅
栤俀丗俹侾偺嵟彫帺慠悢夝(倱丆倲)傪媮傔傛丅
栤俁丗俹乗俀偺嵟彫帺慠悢夝(倶侾丆倷侾)傪媮傔傛丅
栤係丗偙傟傜傪棙梡偟偰丄俹乗俀偺帺慠悢夝(倶俀丆倷俀)丄
(倶俁丆倷俁) 丄(倶係丆倷係)傪媮傔傛丅
栤俆丗師偵丄俹乗俀偺堦斒夝(倶倠丆倷倠)傪丄倠傪梡偄偰昞偣丅
栤俇丗傑偨丄倶俀亅俀倷俀亖侾偺堦斒夝(倶倠丆倷倠)傪丄倠傪梡偄偰昞偣丅

 E-mail
E-mail
 栠傞
栠傞