| NO.1563 | 2005.12.5 | Junko | 規則性の発見(2) |
問１：
f(1)=f(0)+1=1
f(2)=f(1)=1
f(3)=f(1)+1=2
f(4)=f(2)=1
f(5)=f(2)+1=2
f(6)=f(3)=2
f(7)=f(3)+1=3
f(8)=f(4)=1
問２：
０以上の整数ｋに対して
f(2k)=f(2k-1)=･･･=f(1)=1
f(2k-1)=f(2k-1-1)+1=･･･=f(2-1)+(k-1)=k
問３：
100=1100100(2)
f(100)=f(50)=f(25)=f(12)+1=f(6)+1=f(3)+1=f(1)+2=3
問４：
ここで定義されているf(n)という関数は、２進数表示をした際の１の個数を与えるものである。
f(n)=4 となるものは、２進数表示をしたときに、１が４つあるものだから、小さい方から
1111(2)=15
10111(2)=23
11011(2)=27
11101(2)=29
問５：
1024=10000000000(2)
2047=11111111111(2)
f(n)=4 となるものは、２進数表示をしたときに、１が４つあるものを大きい順に書くと、
11110000000(2)
11101000000(2)
11100100000(2)=1824
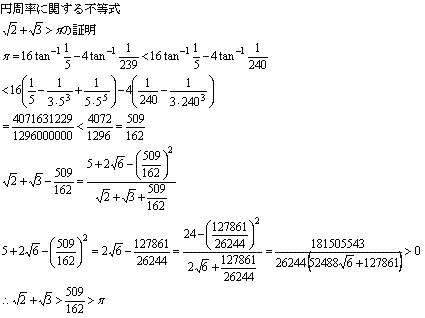
| NO.1564 | 2005.12.6. | 松井 満 | 円周率に関する不等式(3) |
| NO.1565 | 2005.12.6. | 水の流れ | 遺言書 |
皆さん、2005年慶応義塾大学総合政策学部の入試問題に昔からある有名な問題が出題されていました。考えてください。
Ｐ氏はＮ頭のらくだを３人の息子に分けるように遺言して亡くなった。その遺言書によればＮのｘ分の１，ｙ分の１、ｚ分の１
（ｘ、ｙ、ｚは自然数で、ｘ＞ｙ＞ｚとする）が息子たちの相続するらくだの数である。ただし、Ｎはｘ、ｙ、ｚのいずれの倍数でもない。
１／ｘ＋１／ｙ＋１／ｚ＝１ でないので３人は悩んでいると、通りがかりの旅人が良い工夫を思い付いた。
旅人のらくだを１頭を加えてＮ＋１を遺言の率に従って分割すれば、うまく分割でき、１頭余る。
したがって、旅人はなんの損得を受けないとう案である。３人は喜んでこの提案を受け入れた。ここで問題です。（質問を改題）
問題１：一番小さい自然数Ｎとｘ、ｙ、ｚを求めよ。
問題２：２番目に小さい自然数Ｎとｘ、ｙ、ｚを求めよ。
問題３：１００以下の自然数で題意を満たすＮとｘ、ｙ、ｚを求めよ。
問題４：何か考察できたら教えてください。
注）この記事に関する投稿の掲載は、１２月２６日以降とします。
| NO.1566 | 2005.12.25. | 水の流れ | 西暦２００６年 |
来年は西暦２００６年です。
因数分解をすると、２×１７×５９になります。そこで、２００６に関する問題を考えました。
問題１：１，２，３，４，５，６，７，８，９という数字に間に四則演算記号の＋、−、×、÷、さらに（ ）、または数字に間に演算記号を入れなくても良い。すなわち二桁とか、三桁として使用して、
計算式を作り結果が２００６になるようにつくってください。＜いわゆる『小町算』と呼ばれるもの＞
問題２：４という数字を４つ使って、２００６になるようにつくってください。＜いわゆる Four Fourth 問題＞
可能な記号としては、平方根の√ 、階乗の！ 、小数点の「 ．」例えば０.４＝.４ 、０..４＝..４、
循環小数記号の「′」０．４４４・・・＝．４′ があります。
問題３：１連続する幾つかの自然数の和が２００６になるようにつくってください。
問題４：数列１，３，６，10 ，・・・，n(n+1)／２ を三角数といいます。
そこで、３個の三角数の和で２００６になるようにつくってください。
問題５：数列０，１，４，９，16 ，・・・，ｎ×ｎ（ｎは整数） を四角数といいます。
そこで、４個の四角数の和（同じ四角数を何度用いても良い）で２００６になるようにつくってください。
問題６：西暦２００６年は平成１８年にあたります。分数１８／２００６を２つの単位分数の和に分解してください。
注１：フランス人ピエール・ド・フェルマーはディファントスが書いた『算術』の余白に問題４，問題５に関しての記述をしている。
注２：太郎さんには、未だ解決していない問いもあり、不可能なこともありえます。
注３：この記事に関する投稿の掲載は、１月１０日以降とします。
E-mail
戻る