| NO.1557 | 2005.11.12. | Junko | 「算数と数学のだいごみ」 |
秀和システムから、第２弾、
「ポケット図解 教科書とはひと味違う 算数と数学のだいごみ」という本を出版しました。
今回は、教科書とはひと味違う楽しい算数・数学の話をたくさん盛り込みました。柴田さんのイラストがとても可愛くて、私自身も大変うれしく思っています。
是非お読みいただいた感想などいただけると嬉しく思います。
| NO.1558 | 2005.11.14. | Junko | 累乗の和(2) |
問題１
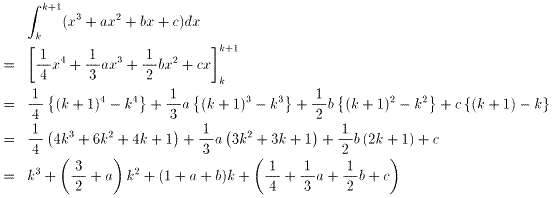
であり、恒等式
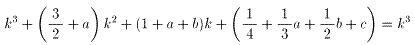
が成り立つことから、
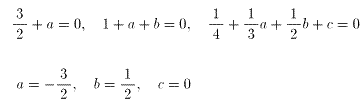
よって、与えられた式は、
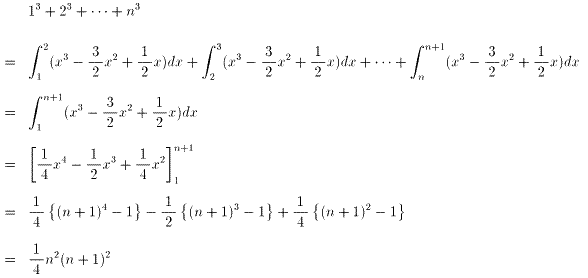
問題２
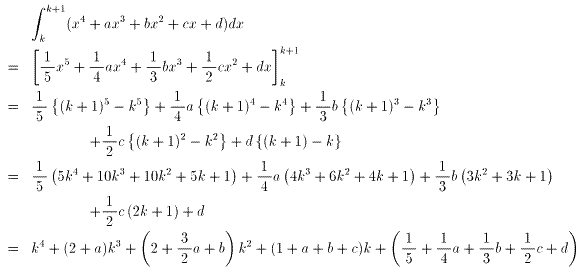
であり、恒等式
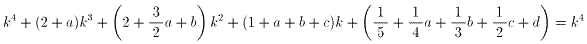
が成り立つことから、
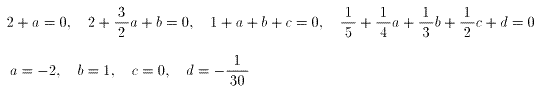
よって、与えられた式は、
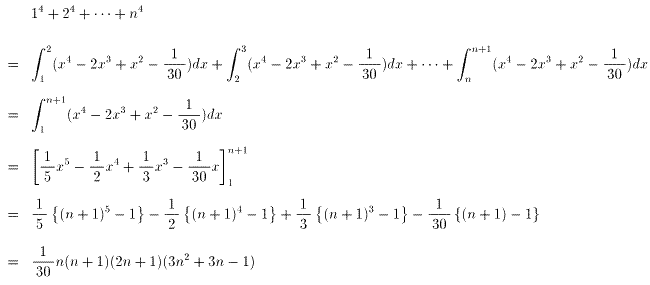
| NO.1559 | 2005.11.14. | 水の流れ | 規則性の発見 |
皆さん、2001年日本大学生産工学部の入試問題からヒントを得て出題しました。考えてください。
０以上の整数ｎに対してｆ（ｎ）は次の条件を満たすものとする。
【条件１】ｆ（０）＝０
【条件２】ｎが偶数のとき、ｆ（ｎ）＝ｆ（n/2）
【条件３】ｎが奇数のとき、ｆ（ｎ）＝ｆ（（n-1）/2）＋１
このとき、次の問に答えよ。
問１：ｆ（２），ｆ（３），ｆ（７），ｆ（８）の値を求めよ。
問２：０以上の整数ｋに対してｆ（２ｋ），ｆ（２ｋ-1）の値を求めよ。
(* 問題文の訂正 11/14 21:00）
問３：100を２進法で表わしなさい。また、ｆ（100）の値を求めよ。
問４：ｆ（ｎ）＝４となるｎを小さいものから順に４つ求めよ。
問５：１０２４≦ｎ≦２０４７とするとき、ｆ（ｎ）＝４となるｎのうち３番目に大きいものを求めよ。
注）この記事に関する投稿の掲載は、１２月５日以降とします。
| NO.1560 | 2005.11.20. | 水の流れ | 円周率に関する不等式(1) |
友人から、次のような問題を頂きましたから、コロキウム室に投稿
します。
問題：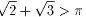
（円周率） を証明せよ。
| NO.1561 | 2005.11.27. | 夜ふかしのつらいおじさん | 円周率に関する不等式(2) |
円周率に関する不等式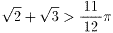 
について
コロキウム室NO.1560円周率に関する不等式：
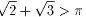は難しそうなので少しゆるめた標記の不等式について書きます。
使うのは、『曲線の凸の部分で外接している線分は、弧よりも長い』ということです。
（図１で、ＡＣ＋ＣＢ＞弧ＡＢ）
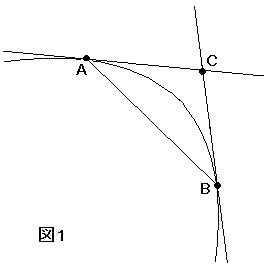
このことを円に当てはめてみます。
図２は、円ｘ２＋ｙ２＝ｒ２上の
点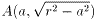 
とＢ（ｒ，０）での接線を示しています。
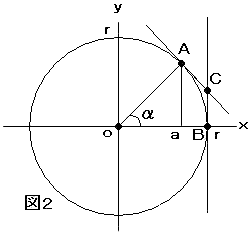
先ずＡＣ＋ＣＢ（＝２ＣＢ）の長さを求めます。
円の式の両辺を微分して ｙ’＝−ｘ／ｙ
だから、接線ＡＣは、
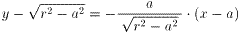
また、接線ＢＣは、
ｘ＝ｒ
この２つの式を連立させて、交点Ｃの座標を求めると、
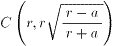
だから、
ＡＣ＋ＣＢ＝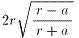
です。
また、弧ＡＢは、ｒαです。だから
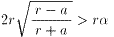
です。ここでｒ＝１とすると、
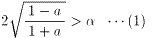
さて、（１）において、
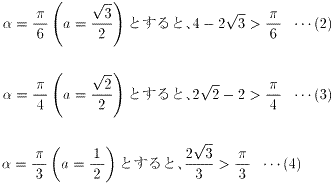
よって、｛（２）＋２×（３）＋９×（４）｝／４を計算すると
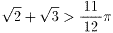
を得ます。
| NO.1562 | 2005.11.28. | 万物流転 | 「算数と数学のだいごみ」(2) |
最近、偉い数学の先生方が、数学の必要性や重要性をやたら強調している。で、何が何でも数学を勉強させたいのか、「数学の授業時間をもっと増やせ」とか「数学を入試必須科目にせよ」などと主張している。だが、そういう押し付けがましい方法で数学を勉強させたとしても、おそらくいい結果は生まれない。むしろ数学嫌いの人が増えるのではないか。
僕が思うに、本当に数学をわかっている人というのは、その必要性や重要性を無駄に強調したりはしない。そういうことをしなくても、数学のおもしろさや魅力を学ぶ側に伝えることができるものだ。それが、現実において役に立つものであるかどうかはわからないが、たとえ役に立たなくても、数学のおもしろさや魅力を何かしら感じ、好きになることができれば、試験や政治の力で強制されなくても、さらに学んでみたくなるものだ。
僕は子供の頃からずっと野球をやってきたが、誰かから強制されて始めたわけじゃない。野球のおもしろさや魅力に惹かれたから始めて、好きだから続けてこれた。野球が「役に立つ」と意識したことはない。「役に立つ」の意味にもよるが、僕は野球で生計を立ててるわけじゃないから、そういう意味では野球は役に立っていない。でも、好きだからやりたいんだよね。役に立たなくてもいいから、自分の人生に潤いを与えるものとして自分が惹かれた野球の素晴らしさを子供たちにも伝えたい。今、僕は子供たちに野球を教えているが、そういう動機からだ。で、教える時は、あまり最初から押し付けがましいことは言わないようにしている。それではもうその時点で野球のおもしろさや魅力が見失われてしまう可能性もあるからだ。まずは野球を楽しみ、好きになってもらい、それに夢中になる過程で自然と野球の基本みたいなものも身に付けてくれたらと願っている。
数学も同じだろう。好きになり、それに夢中になって取り組む中でいろいろなことを学んでいけばいい。だから大事なのは、数学を強制することじゃなくて「数学のおもしろさや魅力を伝えたい」という純粋な気持ちと、その気持ちを実践として表すことじゃないかな。数学が苦手な人や嫌いな人たちに向かって、ただ「数学の必要性を理解できないなんて…」などと嘆いてみたところで反発されるだけさ。そんなことを言う前に「自分が数学嫌いな人を数学ファンに変えてみせる」という気概と行動を見せてみろよ。それこそが数学の専門家が「数学の専門家」と言われる所以じゃないのか。
『ドカベン』という野球アニメで、岩鬼という三振王の選手が、野次られながらも余裕の笑みを浮かべ、打席でこんなことを呟くシーンがある。
〜スーパースターにはアンチもまた付きものや。けど、わいはその実力でアンチたちもしびれさせてファンに変えてきたんやで！〜
たかがアニメの一コマにすぎないが教訓となる内容を含んでいる。自分をスーパースターだなんて自惚れることはできないけどね（笑）。アンチ数学の人がいたっていいじゃないか。それを怒っても数学のおもしろさや魅力を語ることができなければ逆効果さ。怒る前にそんな人たちの心も動かすような数学を提示してみよう。そのための努力の積み重ねこそがアンチ数学の人たちの意識を変え、自分の人間としての器も大きくするんだ。
今回、小島先生の本を読み好きになれたのは、偉い数学の先生方にありがちな嫌味な所が全然ないことだ。「数学が苦手で大嫌い…？気にしないで。私がそんな皆さんを数学ファンに変えてみせましょう！」という強い気持ちが感じられる。今回出された本は、そんな気持ちを示そうと頑張った成果の一つであると思える。それゆえにアンチ数学の人たちをも包み込む温かさと器の大きさも感じられる。自分の数学に対する価値観と異なるそれを持つ人の存在を憂うのではなく、自らが率先して肩肘張らずに数学のおもしろさや魅力をやさしく語り、そういう人たちの考えを変えてみせようという心意気に共感する。数学が好きな人は勿論だが、数学が苦手な人・嫌いな人・受験数学で疲れてしまった人たちにも読んでもらえたらと思う一冊である。と同時に、久しぶりに「素晴らしい数学の先生の存在を知ることができた」と心から思えた。そんな小島先生のこれからの活躍にも期待したい。
野球と数学（それ以外のことでも）。異質なものだが、それに魅せられ、「これからの人にも伝えたい」と願う者が持たなければならない心とその実践は一緒なのだ。
E-mail
戻る