| NO.1553 | 2005.9.5. | 佐野允信 | 綺麗な不等式(2) |
z1,z2,・・・,zn>0とする。
ただし、n≧2とする。
| (z1-z2)2 | +(z1-z3)2 | +(z1-z4)2 | +・・・ | +(z1-zn)2 | |
| +(z2-z3)2 | +(z2-z4)2 | +・・・ | +(z2-zn)2 | ||
| ・・・ | |||||
| +(zn-1-zn)2 | n≧0 ・・・(1) | ||||
が成り立つ。等号の成立は、
z1=z2=z3=・・・=zn ・・・(2)
のときである。
(1) ←→(z12+z22+・・・ +zn2)(n-1)
−2(z1z2+z1z3+・・・+z1zn+z2z3+z2z4+・・・+z2zn+・・・+zn-1zn)≧0
←→(z12+z22+・・・ +zn2)(n-1) ≧2(z1z2+z1z3+・・・zn-1zn) ・・・(3)
また、
(z1+z2+・・・+zn)2=(z12+z22+・・・ +zn2)
+2(z1z2+z1z3+・・・+z1zn+z2z3+z2z4+・・・+z2zn+・・・+zn-1zn) ・・・(4)
より、
z12+z22+・・・ +zn2=(z1+z2+・・・+zn)2−2 (z1z2+z1z3+・・・zn-1zn) ・・・(5)
(3)+(5)より、
n(z12+z22+・・・ +zn2)≧ (z1+z2+・・・+zn)2 ・・・(6)
が成り立つ。
問題4
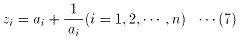
を(6)に代入すると、
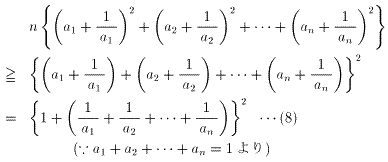
が成り立つ。(2)より、等号の成立は、、
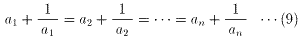
のときである。また、
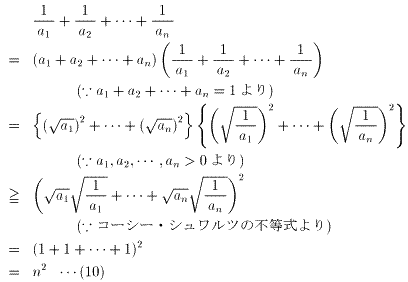
が成り立つ。等号の成立は、
a1=2=・・・=an ・・・(11)
のときである。(8)(10)より、
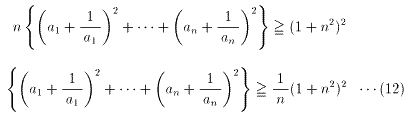
(9)(11)より、等号の成立は、
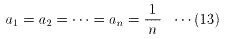
以上より、求めるNの最大値は、
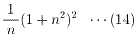
である。
問題1 (12)に、n=2を代入すると、
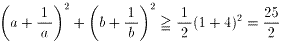
(13)より、等号の成立は、
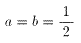
のときである。ここで、
a1=a、a2=b
とした。
問題2 (12)に、n=3を代入すると、
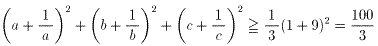
(13)より、等号の成立は、
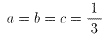
のときである。ここで、
a1=a、a2=b、a3=c
とした。
問題3 (12)に、n=4を代入すると、
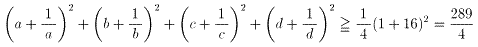
(13)より、等号の成立は、
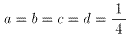
のときである。ここで、
a1=a、a2=b、a3=c、a4=d
とした。したがって、求めるNの最大値は、
289/4
である。
参考文献
「新装版 数学発想ゼミナール3」
L.C.ラーソン著 秋山仁/飯田和 訳
p.342、p.375

| NO.1554 | 2005.9.8. | 水の流れ | 2桁の自然数 |
皆さん、今回は今年度行われた「皇學館大学」の入試問題です。
2桁の正の整数10a+bがある。この整数の十の位の数aと一の位の数bとの和a+bと、
もとの2桁の整数との積はa3+b3に等しい。このとき、次の問に答えよ。
(1)aとbの間の関係式を求めよ。
(2)aとbの大小関係を調べよ。
(3)もとの2桁の整数を求めよ。
注)この記事に関する投稿の掲載は、9月26日以降とします。

| NO.1555 | 2005.9.25. | 水の流れ | 宝さがし |
AB=ACの二等辺三角形ABCの土地があります。太郎さんはAP+BP+CPの長さが最小になる点Pに宝物を埋めました。
宝物が埋まっている点Pがどこか考えてください。ただし、頂角∠BACは120°以内とします
注)この記事に関する投稿の掲載は、10月24日以降とします。

 E-mail
E-mail
 戻る
戻る