コロキウム室

NO.1542

2005.7.4.

佐野允信

放物線の長さ(2)

問題２

求める放物線の長さを とすると

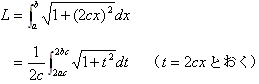
と表せる。

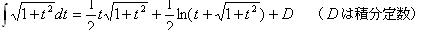
より

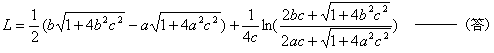
問題１
問題２の結果に，a=0，b=1，c=1 を代入すればいい．
よって、求める放物線の長さは，

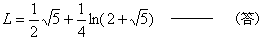
（補足）

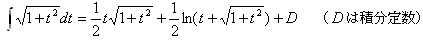
を示す。

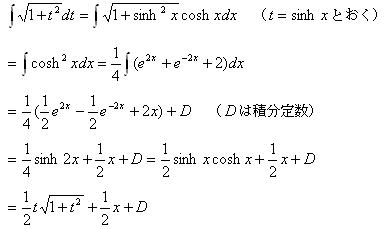
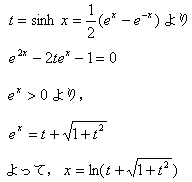
したがって，

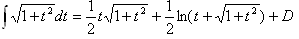
NO.1543

2005.7.4.

夜ふかしのつらいおじさん

放物線の長さ(3)

問題１：
(1/4)log_e(2+√5)＋(√5)/2≒1.47894･･･

問題２：
(1/4c)log_e{(2cb+√(4 c² a²+1))/(2ca+√(4 c² a²+1))} ＋1/2 {b √(4 c² b² + 1)−a√(4 c² b² + 1)}

まず、放物線ｙ＝ｃｘ²の原点Ｏから点Ａ(a,ca²)の長さを求めます。
放物線にそった微小変量をdsとします。
曲線の長さをＬとすると、

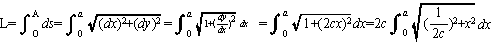
ここで、ｘ＝(1/2c)tanθ と置く。
すると、dx＝(1/2c)･1/(cosθ)²･dθ、
ｘ：０→a　から　θ：０→α(ただし、tanα＝2ca)なので、

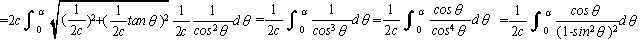
ここで、sinθ＝ｔ と置く。
すると、cosθ dθ＝dt 、
θ：０→α　から　ｔ：０→Ｔ（ただしＴ＝2ca/(√(4 c-2 a²＋１))）

この（Ａ）の式で、ｃ＝ａ＝１とすると、問題１、この式（Ａ）のａをｂに変えたものから（Ａ）を引くと問題２の解答が得られます。

NO.1544

2005.7.4.

蜘蛛の巣城

放物線の長さ(4)

ひょっと解いてみる気になりました。

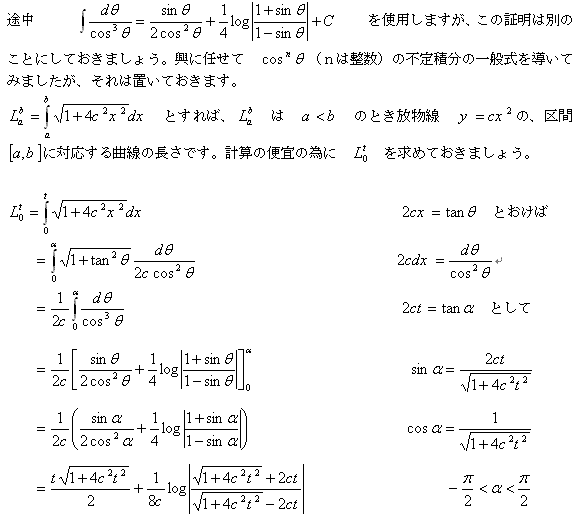
得られた値は　ｃ　の符号の反転に影響は受けません。（当然ですね。でなきゃ困ります）
さて、ａ＜ｂのとき

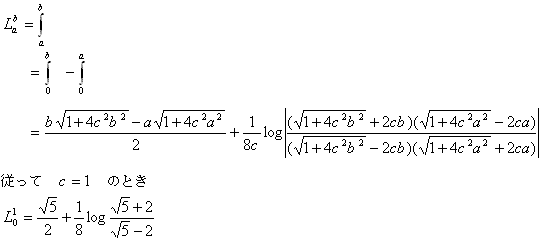
NO.1545

2005.7.4.

水の流れ

オイラー関数

第１５７回数学的な応募問題

皆さん、オイラー関数って知っていますか。今回はこの性質を利用しながら考えてください。

「オイラー関数」

問題１

（１）φ（ｎ）＝８を満たす自然数ｎを求めよ。
（２）φ（ｎ）＝２０を満たす自然数ｎを求めよ。

問題２：

１００より小さくて、１００と互いに素なすべての自然数Ｍについて

（１）この自然数Ｍの個数を求めよ。
（２）この自然数Ｍの和を求めよ。

問題３：

（１）２０のすべての正の約数ｄについて、φ（ｄ）の値を合計するといくつか。
（２）１００のすべての正の約数ｄについて、φ（ｄ）の値を合計するといくつか。
（３）一般に、自然数ｎのすべての正の約数ｄについて、φ（ｄ）の値を合計するといくつか。

注）この記事に関する投稿の掲載は、７月２４日以降とします。

NO.1546

2005.7.23.

DDT

根空間への分解定理

１．根空間への分解定理

ここでいう根空間とは、ベクトル空間の中で定義される次のような部分空間です。ベクトル空間Ｖの次元を、

ｄｉｍ（Ｖ）＝ｎ

線形変換Ａ（行列Ａ）を、

Ａ：Ｖ　→　Ｖ

として、 （Ａ−λ_iＥ）^miｘ＝０

で定義されるベクトルx∈Ｖの全体Ｖ_iのことです。ここでλ_iは、一般的にはある体の要素であり、ＥはＡと同じ次元の単位行列で、ｍ_iとｎは0以上の整数 ｍ_i≦ｎです。これを、

（Ａ−λ_iＥ）^miＶ_i＝｛０｝

と表します。Ｖ_iが、固有値λ_iに属する高さのｍ_iの根空間Ｖ_iです（ｍ_i＝1なら固有空間）。「根空間への分解定理」とは、次の定理をさします。

定理1．（根空間への分解定理）

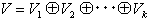
が成り立つ。ここで(Ｖ_i)_i=1〜kは、固有値λ_iに属する高さのｍ_iの根空間Ｖ_iであり、

ｍ_１＋ｍ_２＋・・・＋ｍ_ｋ＝ｎ

となる。ただしは、部分空間の直和を表す。

定理1．は固有ベクトル空間への分解定理の原型であり、線形代数を使って、何故固有ベクトルを計算するかの動機付けを与えるものです。かつこの定理は、初等線形代数の一つの山場であるはずです（陰関数定理が、初等解析の山場であるように）。
定理1．は通常、次の三つの前提から導かれると思います。

1) Cayley-Hamiltonの定理．
2) 互いに素な消去多項式の核空間の独立性．
3) ユークリッドの互除法．

定理1.は初等線形代数の山の一つであるはずなのに、1)〜3)を前提とすると、その証明が全然「線形代数っぽくない」というのがここでの趣旨です。ここには個人的な偏見が存在しています。その偏見とは、

行列やベクトルの線形性と、計量行列の対称性のみから結論を出すのが線形代数だ！

(偏見a)

というものです。上記偏見に従うと1)〜3)には、一般代数系からの密輸入があり過ぎるような気がします。ただし線形代数も代数なので、ある程度の一般代数系の知識は必要です。
そこで、最低限の一般代数系からの密輸入だけで定理1．を証明できないか？という話です。結論は、以下となりました。

1) Cayley-Hamiltonの定理（天下りに認める！。この定理は線形代数の外にある！）．
2) 互いに素な消去多項式の核空間の独立性（簡単なので、これくらいは認める）．
3) 後は、ベクトルの線形性だけで片付ける．ユークリッドの互除法は不要！．

以下、順番に様子をみてみます。

２．Cayley-Hamiltonの定理
Cayley-Hamiltonの定理は、高校数学でも半分おなじみのものだと思います。
それは、行列Ａ（線形変換Ａ）の特性多項式を、

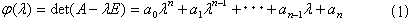
とした場合、形式的にλをＡにおきかえたψ(Ａ)が実は、



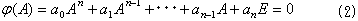
になるという定理です。この証明は初等的には以下となります（「線形代数，伊里正夫，韓大舜，1979年，教育出版株式会社」を使いました）。まず行列 Ａ−λＥ の随伴行列 agj(Ａ−λＥ)を、



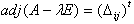
で定義します（^tは転置）。ここでΔ_ijは、δ_ijをクロネッカーのデルタとして、



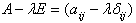
の成分 a_ij−λδ_ij の余因子です。余因子の定義より、agj(Ａ−λＥ) の成分は、λの(n-1)乗以下の多項式です。よってagj(Ａ−λＥ) は、Ａ₀〜Ａ_n-1を適当な定数行列（λを含まない）として、



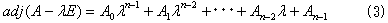
と表せます。一方、行列式のラプラス展開を考慮すると、



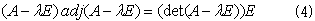
となるので（クラーメルの公式のもと）、(1)と(3)より、



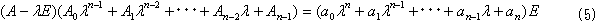
となり、式(5)の両辺でλⁱの係数行列を比べると、



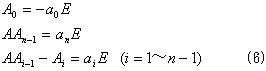
が得られます。(6)を漸化式と考えて順番に代入して行くと、最後には(2)に達する（証明終）。 以上が初等的な（狭義の線形代数の範囲内での）Cayley-Hamiltonの定理の証明の粗筋ですが、これでは「何故かわからいが漸化式を作ってみたら、(2)に達してしまった」としか言えないと思います。ここで「狭義の線形代数」とは、足が3本以上立つテンソル解析を含まないという意味です。もちろん狭義の線形代数においても行列式計算（交代化演算）は必須ですから、「ラプラス展開を考慮する」ことは正当ですし、漸化式(6)を作る動機付けも、ラプラス展開を考慮した関係(4)が成り立つので「やってみるのも悪くない」とは言えます。しかし「偏見(a)」を満たしてくれません。
交代化演算は結局多重線形関数なんだから「偏見(a)」を満たしてるじゃないかと言われれば、それまでなのですが、少なくとも(1)〜(6)には行列やベクトルの線形性が陽に現れていません。また、次の偏見(b)にも抵触します。

証明とは、それが手に取るようにわかった時が証明だ！

(偏見b)

つまり、もし漸化式(6)を作るなら、その動機付けが完璧でなければ嫌です（← 我がままだ！）。「やってみるのも悪くない」くらいでは納得できません。個人的には、狭義の線形代数の内部で、ついにこれは解決できませんでした。
後日難しい代数系の本を斜め読みした結果では、Cayley-Hamiltonの定理は、

1) スカラー上の多項式環（特性多項式） 2) 行列多項式環（Cayley-Hamiltonの定理）

の間の準同型対応から直接出てくるような印象を受けました。図-1が、その準同型対応の概略です。図-1の詳細がわかっていると、Cayley-Hamiltonの定理はある準同型定理の系として、「ポン！」と出てくる（らしい）。この時には、漸化式(6)を作る動機付けも完璧になっている。これは、一般代数系までいってみて初めて手に取るようにわかる、ことを意味します。というわけで、Cayley-Hamiltonの定理は、狭義の線形代数の外にあると思います。なので「天下りに認め」て「これ以上は関りません」。
（でもどなたか、手に取るような証明を教えてください。お願いします）




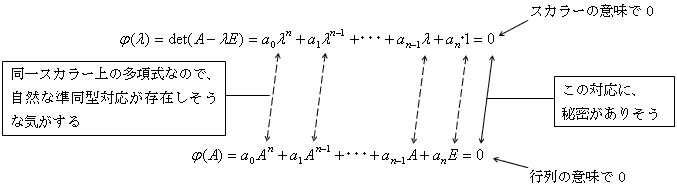
図-1 特性多項式とCayley-Hamiltonの定理の準同型対応の概略

２．互いに素な消去多項式の核空間の独立性
まず核空間を定義します。核空間とは、ベクトル空間ＶからＶ'への線形写像（行列）、

Ａ：Ｖ　→　Ｖ’

に対して、

Ａｘ＝｛０｝

となるx∈Ｖの全体ker(Ａ)のことです。ker(Ａ)は明らかにＶの部分空間で、行列Ａの性質だけからその全体が決まります。そこでker(Ａ)のことを、Ａの核空間と呼びます。
次にベクトルx∈Ｖを0に変換する行列Ａの多項式を、ベクトルxに関する行列Ａの消去多項式と呼びます。いま例えば、



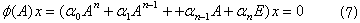
としたとき、行列多項式 φ(Ａ)にＡをかけたＡ･φ(Ａ)においても、Ａ･φ(Ａ)x = Ａ･0 = 0は明らかです。よって消去多項式の次数は、一般に一意には定まりません。そこで最小消去多項式を次のように定義します。

定義1．（最小消去多項式の定義）
式(7)を満たす行列多項式φ(Ａ)のうち最低次数であるものを、ベクトルxに関する行列Ａの最小消去多項式と呼び、

φ_min（Ａ）

で表す。 ベクトルxの消去多項式と最小消去多項式の関係は以下です。

補題1．
ベクトルxの最小消去多項式は、同一ベクトルに対する任意の消去多項式を割り切る。ここで割り切るとは、スカラー上の多項式における割り切る、割り切らない（余りが出る）と同じ意味。

［証明］
ベクトルxの最小消去多項式と消去多項式を、それぞれφ_min(Ａ)，φ(Ａ)とする。

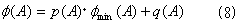
とかける。ここでp(Ａ)はφ_min(Ａ)とφ(Ａ)をＡに関する多項式と考えて、φ(Ａ)をφ_min(Ａ)で割った商で、ある適当な行列Ａの多項式。q(Ａ)はその余りで、やはり行列Ａの多項式。q(Ａ)の次数がφ_min(Ａ)の次数より低いことは明らか（φ_min(Ａ)で割った余りだから）。
式(8)より、



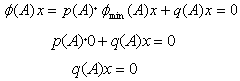
が導ける。ここでq(Ａ)≠0（零行列）とすると、最小消去多項式φ_min(Ａ)よりも次数の低い、ベクトルxの消去多項式が存在することになる。これは最小消去多項式の定義に反する。よってq(Ａ)＝0であるか、x＝0が必要。

1) q(Ａ)＝0の場合、最小消去多項式φ_min(Ａ)は、φ(Ａ)を割り切る。 2) x＝0の場合、xの最小消去多項式が単位行列Ｅのスカラー倍であることは明らか。

従っていずれにしろ、最小消去多項式は、同一ベクトルに対する任意の消去多項式を割り切る。

［証明終］

補題1.から次の補題2.をすぐに得ます。

補題2．
互いに素な行列多項式の核空間は独立。ここで互いに素とは、互いに互いを割り切らない多項式の意味。
［証明］
φ₁(Ａ)，φ₂(Ａ)を行列Ａの多項式として、その核空間を、

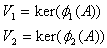
とする。x≠0かつx∈Ｖ₁∩Ｖ₂とすると、φ₁(Ａ)とφ₂(Ａ)はベクトルxの消去多項式になっているから、共通因数として最小消去多項式φ_min(Ａ)を含む。Ｅx≠0は明らかだからφ_min(Ａ)≠Ｅも明らか。よってφ₁(Ａ)とφ₂(Ａ)が互いに素なら、Ｖ₁∩Ｖ₂＝{0}が必要。これはＶ₁とＶ₂が独立な部分空間であることを意味する。

［証明終］

３．線形写像の標準（？）分解（後はベクトルの線形性のみ．ユークリッドの互除法は使わない）
根空間への分解定理を証明するために、あと定義4つと補題を3つ追加します。いずれも簡単なものです。

定義2．（線形写像と線形変換の用語上の区別）
ＶとＶ'を、必ずしも同一とは限らないベクトル空間とする。写像Ａ（行列Ａ）が、


Ａ：Ｖ　→　Ｖ’

で線形であるとき、これをＶからＶ'への線形写像という。とくにＶ'＝Ｖであるとき、Ｖ上の線形変換と呼ぶ。

定義3．（正則線形写像の定義）
ＶからＶ'への線形写像Ａ（行列Ａ）が単射（1対1対応）であるとき、正則と呼ぶ。

定義3.から、次の補題がほぼ自明に出ます。

補題3． 線形な Ａ：Ｖ→Ｖ'が正則である条件は、

ker(Ａ)＝｛０｝

が成り立つこと。

［証明］
Ａ･0＝0は明らか。0∈Ｖ'に写像するx∈Ｖ全体とは、ker(Ａ)のこと。Ａは正則なので単射。よって、Ａ･0＝0より、ker(Ａ)＝{0}である。
逆にker(Ａ)＝{0}とする。xとy∈Ｖとして、Ａx＝Ａyとすれば、

Ａｘ＝Ａｙ
Ａｘ−Ａｙ＝０
Ａ(ｘ−ｙ)＝０


となるので、

ｘ−ｙ∈ker(Ａ)＝｛０｝

でなければならない。これは、

ｘ−ｙ＝０
ｘ＝ｙ


を意味する。従ってＡは単射であり、正則。

［証明終］

定義4．（像空間という用語の定義）
Ａを、ＶからＶ'への線形写像（行列）とする。x∈Ｖとして、Ａx∈Ｖ'のことを、Ａによるxの像と呼ぶ。xをＶの中で任意に動かした時のＡxの全体の集合、

｛y|y∈Ｖ'かつy＝Ａxとなるx∈Ｖが存在する｝

のことを、ＡによるＶの像と呼び、ＡＶで表す。ＡＶ⊂Ｖ'は、Ｖ'の部分空間をなす。ＡＶを、Ａの像空間と呼ぶ。

定義5．（写像の実質部分）
ＸとＹを集合、fを写像（線形でなくても良い）、

ｆ：Ｘ　→　Ｙ


とする。定義4.と同様に、ここでも、f(x)をfによるx∈Ｘの像と呼ぶ。f(x)の全体、

｛y|y∈Ｙかつy＝f(x)となるx∈Ｘが存在する｝

のことを、fによるＸの像と呼び、f(Ｘ)で表す。f(Ｘ)⊂Ｙは明らか。
ところで、Ｙに関するf(Ｘ)の補集合 Ｙ−f(Ｘ) の中には、fでＸから写像してくるものはない。従って、fの値域Ｙをf(Ｘ)に狭めても、実質的にfは変わらないことになる。



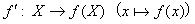
で定義される写像f'のことを、f(Ｘ)への移行によってfから得られる写像という。
次に、Ｚ⊂Ｘの場合も用語を流用して、x∈Ｚのfによる像f(x)の全体のことを、やはりf(Ｚ)と書く。f(Ｚ)⊂f(Ｘ)⊂Ｙ。このとき、fの定義域ＸをＺに狭めて得られる写像f"、



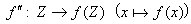
のことを、やはり用語を流用して、Ｚとf(Ｚ)への移行によってfから得られる写像という。

f'やf"が全射（上への写像）であることは、定義より明らか。

線形写像の基本構造は、補題4.となる。

補題4．（線形写像の基本構造）
Ａ：Ｖ→Ｖ'を線形写像、Ｖに関するker(Ａ)の直和補空間を Ｗ とする。Ｗと、ＡによるＷの像ＡＷ への移行によってＡから得られる写像、



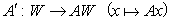
をＡ'で表す。Ａ'に関して以下が成り立つ。

1) ker(Ａ)の直和補空間 Ｗ は必ず存在する。従ってＡ'も必ず存在する。
2) Ａ'は線形写像。従ってＡＷ は Ｖ' の部分空間。
3) Ａ'は正則線形写像。
4) Ｗの基底は、ＡＷの基底に写る。
5) ＡＷ＝ＡＶ。
6) 逆線形写像（逆行列）Ａ'^-1、




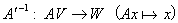
が存在する。

［証明］
1)
ker(Ａ) はＶの部分空間だからベクトル空間であり、ker(Ａ)を張る基底Ｂ_kerが必ず存在する。ただし、Ｂ_ker＝{0}の場合も基底と約束する（これはker(Ａ)＝{0}を意味し、その場合Ａは正則である）。
Ｂ_kerの全てのベクトルと独立で、しかも互いに独立なベクトルを、Ｖの中から最大本数集めてきて、それをＢ_Ｗとすれば、Ｂ_Ｗはある部分空間Ｗの基底であり、Ｗの中の全てのベクトルと、ker(Ａ)の中の全てのベクトルは独立になる。またＢ_Ｗ∪Ｂ_kerは、明らかにＶの基底である。これらは、

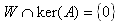
と、



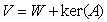
を意味し、



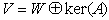
であることが言える。ただし、Ｂ_Ｗ＝{0}の場合も基底と約束する（これはker(Ａ)＝Ｖを意味し、その場合はＡ＝0である）。従って、ker(Ａ)の直和補空間 Ｗ は必ず存在し、Ａ'も必ず存在する。

2)
ＡＷ⊂ＡＶ⊂Ｖ' が Ｖ' の部分空間であるためには、Ａ' が線形写像であれば良い。Ａ'の定義より、x，y∈Ｗ、kをスカラーとすれば、

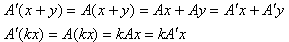
だから、Ａ'は線形写像。

3)
2)より、Ａ'は線形写像だからker(Ａ')は意味を持ち、やはりＡ'の定義より、

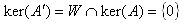
が成り立つ。補題3.より、Ａ'は正則。

4)
Ｂ_Ｗ＝{ｗ₁，ｗ₂，･･･．ｗ_k}をＷの基底とする。 任意のx∈Ｗは、α_i（i＝1〜k）をスカラーとして、

ｘ＝α₁ｗ₁＋α₂ｗ₂＋・・・＋α_kｗ_k

と書ける。

Ａ’ｘ＝Ａ（α₁ｗ₁＋α₂ｗ₂＋・・・＋α_kｗ_k） ＝α₁Ａｗ₁＋α₂Ａｗ₂＋・・・＋α_kＡｗ_k　　　(9)

である。定義5.の最後よりＡ'は全射だったから、ＡＷの任意のベクトルは、式(9)の形をしていなければならない。 これは Ｂ_ＡＷ＝{Ａｗ₁，Ａｗ₂，･･･，Ａｗ_k} で ＡＷ が張られることを意味する。 ただし、Ｂ_ＡＷ のベクトルが全て互いに独立であることは、ただちに明らかではない。次にこれを示す。

α₁Ａｗ₁＋α₂Ａｗ₂＋・・・＋α_kＡｗ_k＝０

とすると、右辺の0が0∈ＡＷなのは自明だから、

α₁Ａｗ₁＋α₂Ａｗ₂＋・・・＋α_kＡｗ_k ＝Ａ（α₁ｗ₁＋α₂ｗ₂＋・・・＋α_kｗ_k） ＝Ａ’（α₁ｗ₁＋α₂ｗ₂＋・・・＋α_kｗ_k） ＝０

より、

α₁ｗ₁＋α₂ｗ₂＋・・・＋α_kｗ_k∈ker（Ａ’）

でなければならないが、3)よりＡ'は正則で、ker(Ａ')＝{0}。従って、

α₁ｗ₁＋α₂ｗ₂＋・・・＋α_kｗ_k＝０

となる。Ｂ_Ｗ＝{ｗ₁，ｗ₂，･･･．ｗ_k}はＷの基底だったから、α_i＝0（i＝1〜k）となる。 これは、Ｂ_ＡＷ＝{Ａｗ1，Ａｗ2，･･･，Ａｗk} のベクトルが全て互いに独立であること意味する。 よって Ｂ_ＡＷ は ＡＷの基底であり、Ｂ_Ｗ がＷの基底なら、Ｂ_ＡＷ はＡＷの基底。

5)

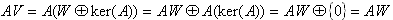
だから。

6)
5)より、ＡＷ＝ＡＶなので、

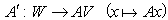
である。線形写像Ａ'は明らかに全射で、3)より単射だった。従ってＡ'は双射（1対1かつ上への写像）であり、逆写像、



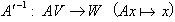
が存在する。これが線形であれば良い。Ａx，Ａy∈ＡＶとすると、逆写像の定義より、

Ａ'^-1(Ａx＋Ａｙ)＝Ａ'^-1(Ａ（x＋y）)＝ｘ＋ｙ

が成り立つが、Ａ'の定義から、Ａ'^-1(Ａx)＝x，Ａ'^-1(Ａy)＝yでもあるから、

Ａ'^-1(Ａx＋Ａｙ)＝Ａ'^-1(Ａx)＋Ａ'^-1(Ａy)

がいえる。同様にkをスカラーとして、

Ａ'^-1(ｋＡx)＝Ａ'^-1(Ａ（ｋx）)＝ｋｘ

から、

Ａ'^-1(ｋＡx)＝ｋＡ'^-1(Ａx)

がいえる。よって逆写像Ａ'は線形。

［証明終］

補題4.は、次の図-2としてまとめられる。図-2を、線形写像Ａの標準分解と呼ぶ（と勝手に呼んでます）。 図-2をとくにＶ'＝Ｖで、ＡがＶ上の線形変換 Ａ：Ｖ→Ｖ の場合で考えると、次の補題5.が得られる。

補題5．
Ａ：Ｖ→Ｖを線形変換とする。Ｖが有限次元の場合、次の3つは同値である。

1) Ａが正則
2) Ａが単射
3) Ａが全射

［証明］ 1) ⇔ 2)

定義3.そのもの。



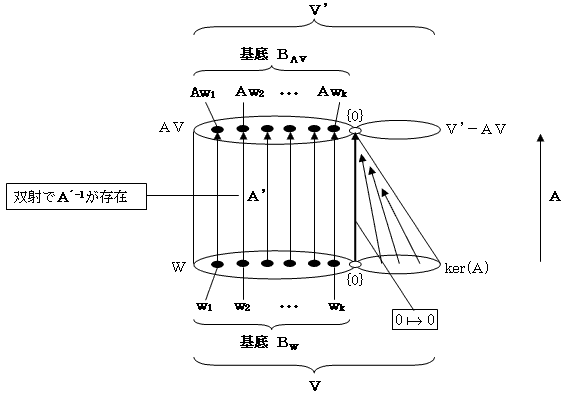
図-2 線形写像の標準分解

1) ⇒ 3)

Ａが正則なら、補題3.よりker(Ａ)＝{0}。これは図-2で、Ｖ'＝Ｖ，Ｗ＝ＶかつＡ'＝Ａとなった場合に相当する。Ａ'はもともとＡＶへの全射だったから、ＡＶ＝Ｖであれば良い。図-2より、それはＡＶの基底Ｂ_ＡＶ がＶ'を張ることを意味する。
補題4.の4)より、Ｗの基底Ｂ_Ｗ は ＡＶの基底Ｂ_ＡＶ に写るが、Ｗ＝Ｖであることから、Ｂ_Ｗ はＶの基底Ｂ_Ｖ である。
Ｂ_Ｖ に含まれるベクトルの本数とは、Ｖから集めてこれる独立なベクトルの最大本数のこと（それが基底と次元の定義）。
Ｂ_ＡＶ に含まれるベクトルの本数は、Ｂ_Ｖ に含まれるベクトルの本数に等しい。
いまＶ'＝Ｖに注意すると、Ｂ_ＡＶ に含まれるベクトルの本数は、Ｖ'＝Ｖから集めてこれる独立なベクトルの最大本数に等しい。よってＢ_ＡＶ はＶ'＝Ｖの基底である。これは、Ｖの部分空間ＡＶ⊂Ｖの基底Ｂ_ＡＶ が、Ｖを張ることを意味するから、ＡＶ＝Ｖとなる。従って、Ａは全射。

3) ⇒ 1)

Ａが全射なら、図-2でＡＶ＝Ｖ'＝Ｖだから、逆線形変換、




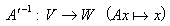
が存在する。逆線形変換も線形写像だから、Ａ'^-1用に図-2を書きなおすと、図-3となる。



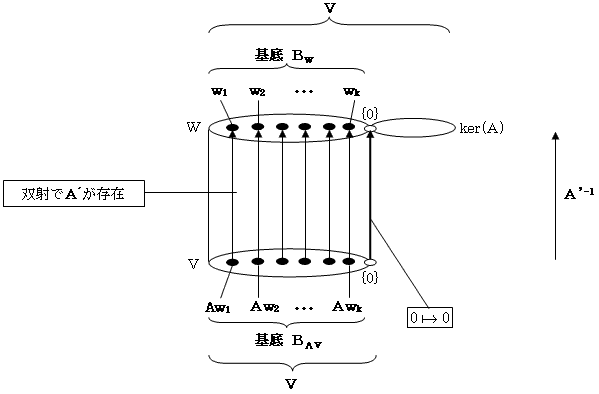
図-3 線形写像の標準分解

図-3と図-2を比較すると、さっきと同様に基底Ｂ_Ｗ がＶを張るのは明らかだから、ker(Ａ)＝{0}である。補題3.より、Ａは正則で単射（お釣りとして、Ａ'＝Ａ）。

［証明終］

以後使用しないが、図-2からは、次の系1.があっさりと出てくる。これも有限次元の線形代数（つまりふつうの線形代数）の基本定理の一つと思えるが、何故か余り注目されません。実際、次元や基底の定義を思い出すと、系1.は、図-2や補題4.と同値です。

系1．
Ａ：Ｖ→Ｖ'を線形写像とする。Ｖが有限次元の場合、次式が成り立つ。

dim(ＡＶ)+ker(Ａ)=dim(Ｖ)

［証明］
図-2より自明。

［証明終］

４．根空間への分解定理の証明
ここで「根空間への分解定理」をもう一度まとめる。次元nのベクトル空間Ｖ上の行列Ａ（線形変換Ａ）の特性多項式が、

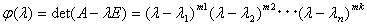
であるとき（ｍ₁＋ｍ₂＋･･･＋ｍ_k＝ｎ）、 ψ(λ)のλを形式的にＡに置き換えたψ(Ａ)において、Cayley-Hamiltonの定理、



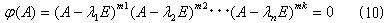
が成り立ち、全空間Ｖは、(Ａ−λ_iＥ)^miの核空間である根空間Ｖ_i、



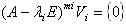
によって、直和分解、



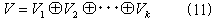
をうけるというものです。
ここで全空間Ｖは、特性多項式ψ(Ａ)の核空間になっています。また根空間Ｖ_iは、ψ(Ａ)の因子である行列多項式(Ａ−λ_iＥ)^miの核空間で、各(Ａ−λ_iＥ)^miは互いに素な行列多項式なので、 Ｖ₁〜Ｖ_kは最初から独立な部分空間になっています（補題2.）。 さらに因子(Ａ−λ_iＥ)^miも、Ａ上の線形変換で、かつ可換なのは明らかです。これらの言葉で(10)と(11)を書き直すと、Ａ_iをＶ上の線形変換として、



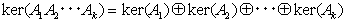
が成り立ち、式(12)が成り立つ条件は、線形変換Ａiが互いに可換で、Ａ_iの核空間ker(Ａ_i)が互いに独立というものです。「根空間への分解定理」を証明するためには、結局次の補題が成り立てば良いことがわかります。

補題6．
Ａ₁とＡ₂をＶ上の可換な線形変換で、核空間が独立とする。すなわち、

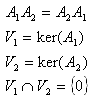
とする。このときＡ₁Ａ₂の核空間を、

Ｖ_０＝ker（Ａ₁Ａ₂）

とすれば、

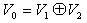
［証明］
Ａ₁とＡ₂が可換だから、

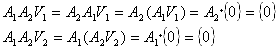
が成り立ち、Ｖ₁，Ｖ₂⊂Ｖ₀で、Ｖ₁とＶ₂はＶ₀の部分空間をなす。 よってＶ₀の中での Ｖ₁＋Ｖ₂ の直和補空間が存在する。それをＶ₃とする。 Ｖ₁とＶ₂はもともと独立なので、



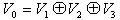
となる。Ｖ₃＝{0}がいえれば良い。 Ａ₁とＡ₂が可換であることより、



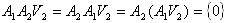
なので、

Ａ₁Ｖ₂⊂Ｖ₂　　　　　(13)

でなければならない。すなわち、Ａ₁はＶ₂上の線形変換になっている。
同様に、



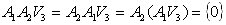
なので、

Ａ₁Ｖ₃⊂Ｖ₂　　　　　(14)

でなければならない。よってＡ₁は、Ｖ₃からＶ₂への線形写像も定義するが、これと(13)を合わせると、 Ａ₁は、Ｖ₂₃Ｖ₃からＶ₂への線形写像にもなっている。
Ｖ₂への移行によってＡ₁から得られる線形写像を考え、 これをＡ₁⁽²⁾と表す。(13)より、Ａ₁⁽²⁾はＶ₂上の線形変換、

Ａ₁⁽²⁾：Ｖ₂　→　Ｖ₂

になる。Ａ₁⁽²⁾の核空間は明らかに、 Ａ₁の核空間Ｖ₁とＶ₂との共通分だが、 これらはもともと独立だったので、



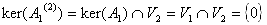
である。従ってＡ₁⁽²⁾はＶ₂上で正則（補題3.）なので全射（補題5.の3)）。よって、



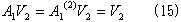
が成り立つ。 次に、Ｖ₂ Ｖ₃への移行によってＡ₁から得られる線形写像を考え、これをＡ₁(2＋3)と表す。(13)と(14)より、これはＶ₂ Ｖ₃からＶ₃への線形写像、



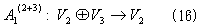
となり、その核空間は、Ａ₁⁽²⁾の場合と同様に、



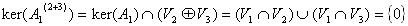
である。Ａ₁(2＋3)は正則であり、独立なベクトルは独立なベクトルに写像されるので（補題4.の4)）、



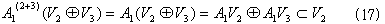
が成り立つ。Ａ₁Ｖ₂⊂Ａ₁ＶSUB>2 Ａ₁Ｖ₃は明らかであるから、(17)より、



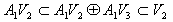
である。(15)を考慮すると、



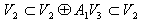
となって、



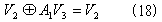
が得られる。(18)から明らかに、Ａ₁Ｖ₃＝{0}なので、



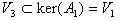
が得られる。Ａ₂とＶ₃に関しても、(19)と同じ関係が得られるので、



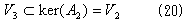
でなければならない。(19)と(20)より、



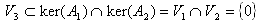
となり、Ｖ₃＝{0}

［証明終］

定理1．（根空間への分解定理）
次元ｎのベクトル空間Ｖ上の線形変換になっている行列Ａの特性多項式を、

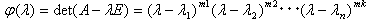
とする（ｍ₁＋ｍ₂＋･･･＋ｍ_k＝ｎ）。 ベクトル空間Ｖは、高さｍ_iの固有値λ_iに属する根空間Ｖ_i、

(Ａ−λ_iＥ)^miＶ_i＝｛０｝

によって、直和分解、



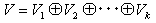
を受ける。ただしは、部分空間の直和を表す。

［証明］
Cayley-Hamiltonの定理より、任意の正方行列Ａについて、

φ（Ａ）＝（Ａ−λ_１Ｅ)^m1（Ａ−λ_２Ｅ)^m2・・・（Ａ−λ_ｋＥ)^mk＝０

が成り立つので、

Ｖ＝ker（φ（Ａ））

である。ψ(Ａ)の各因子(Ａ−λ_i)^miを、

Ａ_i＝(Ａ−λ_i)^mi

と表すことにすれば、

φ（Ａ）＝Ａ₁Ａ₂・・・Ａ_k

とかける。

ker（Ａ₁Ａ₂・・・Ａ_k）＝ker（Ａ₁（Ａ₂Ａ₃・・・Ａ_k））

と分けて考えれば、Ａ₁とＡ₂Ａ₃･･･Ａ_kは、互いに素な行列多項式で可換である。従って補題6)より、



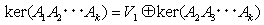
と分解できる（Ｖ₁＝ker(Ａ₁)）。同様に、



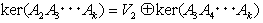
が成り立つ（Ｖ₂＝ker(Ａ₂)）。同じ分解を、(k-2)回繰り返せば、



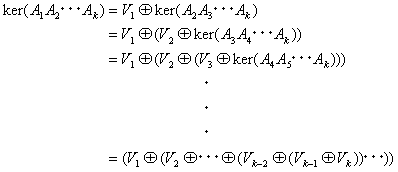
が得られる。Ｖ＝ker(ψ(Ａ))＝ker(Ａ₁Ａ₂･･･Ａ_k)に注意すれば、



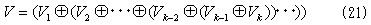
となる。(21)において、ベクトル和は可換なので、



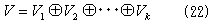
が得られる。

［証明終］

NO.1547

2005.7.24.

夜ふかしのつらいおじさん

オイラー関数(2)

問題１
（１）φ(ｎ)＝8　を満たす自然数ｎは、　15，16，20，24，30

• 直接8として
  
  　　　φ(16)＝φ(2⁴)＝2⁴−2³
  
  
• 2×4として
  
  　　　φ(15)＝φ(3・5)＝φ(3)・φ(5)＝2・4　　（2，4直接）
  　　　φ(20)＝φ(2²・5)＝φ(2²)・φ(5)＝(2²−2)・4　　（2の変形）
  　　　φ(24)＝φ(2³・3)＝φ(2³)・φ(3)＝(2³−2²)・2　　（4の変形）
  　　　φ(30)＝φ(2・3・5)＝φ(2)・φ(3)・φ(5)＝1・2・4　　（φ(2)＝1利用）
  
  

（２）φ(ｎ)＝20　を満たす自然数ｎは、25，33，44，50，66

• 直接20として
  
  　　　φ(25)＝φ(5²)＝5²−5¹
  　　　φ(50)＝φ(2・5²)＝φ(2)・φ(5²)＝1・(5²−5¹)　　（φ(2)＝1利用）
  
• 2×10として
  
  　　　φ(33)＝φ(3・11)＝φ(3)・φ(11)＝2・10　　（2，10直接）
  　　　φ(44)＝φ(2²・11)＝φ(2²)・φ(11)＝(2²−2¹)・10　　（2変形）
  　　　φ(66)＝φ(2・3・11)＝φ(2)・φ(3)・φ(11)＝1・2・10　　（φ(2)＝1利用）
  
  ※　φ(ｋ)＝P（Pは2以外の素数）となる自然数ｋは存在しない。
  　　　Pが素数なので性質(３)(４)は当てはまらない。
  　　　（性質の式の右辺が合成数なので）
  　　　また、性質（２）も(P+1)は合成数になり当てはまらない。
  　　　だから、（２）で 20＝4×5 などの可能性はない。
  

問題２：
100＝2²×5² である。
だから、100と互いに素な自然数は、2の倍数でなく、かつ5の倍数でない数である。
（１）100より小さくて、100と互いに素な自然数Ｍの個数は40個。

• 2の倍数は、100÷2＝50 個
• 5の倍数は、100÷5＝20 個
• 10の倍数（2かつ5の倍数）は、100÷10＝10 個

　　 よって、100−(50＋20−10)＝40個

（２）100より小さくて、100と互いに素な自然数Ｍの和は2000。

• 1から100までの自然数の和は、(1/2)・100・(1+100)＝5050
• 1から100までの2の倍数の和は、(1/2)・50・(2+100)＝2550
• 1から100までの5の倍数の和は、(1/2)・20・(5+100)＝1050
• 1から100までの10の倍数の和は、(1/2)・10・(10+100)＝550

よって、5050−(2550＋1050−550)＝2000。

問題３：
（１）２０のすべての正の約数ｄについて、φ（ｄ）の値を合計すると，20
（２）１００のすべての正の約数ｄについて、φ（ｄ）の値を合計すると，100
（３）自然数ｎのすべての正の約数ｄについて、φ（ｄ）の値を合計すると，ｎ

　　　説明はどれでも同じなので、100でやってみる。
　　　100＝2²×5² と素因数分解される。
　　　すると、100 の約数は、次の展開の各項である。

	(1＋2＋22)・(1＋5＋52)
＝	1・1＋1・5＋1・52＋2・1＋2・5＋2・52＋2 2・1＋22・5＋22・52

　　　その値を引数とする、オイラー関数の和を調べる。
　　　ここで、関数の引数は互いに素な２つの数の積になっている。
　　　また、φ(1)＝1 を使う。

	φ(1・1)　＋φ(1・5)　＋φ(1・52) ＋φ(2・1)　＋φ(2・5)　＋φ(2・52) ＋φ(22・1)＋φ(22・5)＋φ(22・52) 　　　（性質（４）より）
＝	φ(1)・φ(1)　＋　φ(1)・φ(5)　＋φ(1)・φ(52) ＋φ(2)・φ(1)　＋　φ(2)・φ(5)　＋φ(2)・φ(52) ＋φ(22)・φ(1)＋φ(22)・φ(5)＋φ(22)・φ(52)
＝	φ(1)・｛φ(1)＋φ(5)＋φ(52)｝ ＋　φ(2)・｛φ(1)＋φ(5)＋φ(52)｝ ＋φ(22)・｛φ(1)＋φ(5)＋φ(52)｝
＝	φ(1)＋φ(2)＋φ(22)｝・｛φ(1)＋φ(5)＋φ(52)｝ 　　　（性質（３）より）
＝	｛1＋(21−20)＋(22−21)｝・｛1＋(51−50)＋(52−51)｝
＝	22・52
＝	100

NO.1548

2005.7.24.

佐野允信

オイラー関数(3)

問題１
ｎ＝２^k（ｋは正の整数）のとき
　　　φ(ｎ)＝２^k−２^k-1＝２^k-1（２−１）＝２^k-1　・・・(1)

ｎ＝２ｌ＋１（ｌは正の整数）のとき
　　　ｎ＝ｐ₁^ｌ₁・ｐ₂^ｌ₂・・・ｐ_m^ｌ_m
　　　（ｌ₁、ｌ₂、・・・、ｌ_mは正の整数；ｐ₁、ｐ₂、・・・、ｐ_mは奇素数；ｐ₁＜ｐ₂＜・・・＜ｐ_m）　・・・(2)

と表せる。ｐ_k（ｋ−１，・・・，ｍ）は奇数だから、

　　　ｐ_k＝２Ｓ_k＋１（Ｓ_kは正の整数；ｋ＝１，２，・・・，ｍ）　・・・(3)

と表せる。よって、

　　　φ(ｎ)＝ｐ₁^ｌ₁-1（ｐ₁−１）・ｐ₂^ｌ₂-1（ｐ₂−１）・・・ｐ_m^ｌ_m-1（ｐ_m−１）
　　　＝２^mＳ₁Ｓ₂・・・Ｓ_m ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1・・・ ｐ_m^ｌ_m-1　・・・(4)

従って、ｎ＝２ｌ＋１（ｌは正の整数）のとき、φ(ｎ)は偶数である。

(1)
(i)ｎ＝２^k（ｋは正の整数）のとき
　　　φ(ｎ)＝２^k-1　　（∵(1)より）
　　　　　　＝２³　・・・(5)
∴　ｋ＝４
∴　ｎ＝２^４＝１６　・・・(6)

(ii)ｎ＝２ｌ＋１（ｌは正の整数）のとき
　　　φ(ｎ)＝２^mＳ₁Ｓ₂・・・Ｓ_m ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1・・・ ｐ_m^ｌ_m-1　（∵(4)より）
　　　　　　＝２³　・・・(7)
従って、１≦ｍ≦３でなければならない。

（ア）ｍ＝１のとき
　　　φ(ｎ)＝２Ｓ₁ｐ₁^ｌ₁-1＝２³
　　∴　Ｓ₁＝２²　かつ　ｌ₁＝１　・・・(8)
このとき、
ｐ₁＝２Ｓ₁＋１＝９
となり、ｐ₁が素数であることに矛盾する。

（イ）ｍ＝２のとき
　　　φ(ｎ)＝２²Ｓ₁Ｓ₂・ ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1 ＝２³
∴　ｌ₁＝ｌ₂＝１　かつ　Ｓ₁Ｓ₂＝２
Ｓ₁＜Ｓ₂より、（Ｓ₁,Ｓ₂）＝（１，２）　・・・(10)
このとき、
ｐ₁＝２Ｓ₁＋１＝３
ｐ₂＝２Ｓ₂＋１＝５
となり、ｐ₁、ｐ₂は奇素数になる。
∴　　ｎ＝ｐ₁^ｌ₁・ｐ₂^ｌ₂＝３×５＝１５　・・・(11)

（ウ）ｍ＝３のとき
　　　φ(ｎ)＝２³Ｓ₁Ｓ₂Ｓ₃・ ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1 ・ｐ₃^ｌ₃-1 ＝２³
∴　ｌ₁＝ｌ₂＝ｌ₃＝１　かつ　Ｓ₁Ｓ₂Ｓ₃＝１　・・・(12)
Ｓ₁Ｓ₂Ｓ₃＝１より、 （Ｓ₁,Ｓ₂,Ｓ₃）＝（１，１，１）となり、 Ｓ₁＜Ｓ₂＜Ｓ₃に矛盾する。

(iii)ｎ＝２^k（２ｌ＋１）（ｋ，ｌは正の整数）のとき
　　　φ(ｎ)＝φ（２^k）φ（２ｌ＋１）
　　　　　　＝２^k-1・φ（２ｌ＋１）
　　　　　　＝２³

φ（２ｌ＋１）は、偶数だから、０≦ｋ−１≦２、すなわち、１≦ｋ≦３でなければならない。

（ア）ｋ＝１のとき
　　　φ（２ｌ＋１）＝２³　・・・(14)
(11)より、２ｌ＋１＝１５　・・・(15)
∴　ｎ＝２×１５＝３０　・・・(16)

（イ）ｋ＝２のとき
　　　φ（２ｌ＋１）＝２^mＳ₁Ｓ₂・・・Ｓ_m ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1・・・ ｐ_m^ｌ_m-1　（∵(4)より）
　　　　　　　　　　＝２²　・・・(17)

従って、１≦ｍ≦２でなければならない。

(a)ｍ＝１のとき
　　　φ（２ｌ＋１）＝２Ｓ₁ｐ₁^ｌ₁-1＝２²
∴　　Ｓ₁＝２　かつ　ｌ₁＝１　・・・(18)
このとき、
　　　ｐ₁＝２Ｓ₁＋１＝５
となり、ｐ₁は奇素数になる。
∴　２ｌ＋１＝ｐ₁^ｌ₁＝５　・・・(19)
∴　ｎ＝２²・５＝２０　・・・(20)

(b)ｍ＝２のとき
　　　φ（２ｌ＋１）＝２²Ｓ₁Ｓ₂ ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1 ＝２²
∴　　ｌ₁＝ｌ₂＝１　かつ　Ｓ₁Ｓ₂＝１　・・・(21)
Ｓ₁Ｓ₂＝１より、（Ｓ₁,Ｓ₂）＝（１，１）となり、 Ｓ₁＜Ｓ₂に矛盾する。

（ウ）ｋ＝３のとき
　　　φ（２ｌ＋１）＝２^mＳ₁Ｓ₂・・・Ｓ_m ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1・・・ ｐ_m^ｌ_m-1　（∵(4)より）
　　　　　　　　　　＝２　・・・(22)

従って、ｍ＝１でなければならない。
　　　φ（２ｌ＋１）＝２Ｓ₁ｐ₁^ｌ₁-1＝２
∴　　Ｓ₁＝１　かつ　ｌ₁＝１　・・・(23)
　 このとき、
　　　ｐ₁＝２Ｓ₁＋１＝３
となり、ｐ₁は奇素数になる。
∴　２ｌ＋１＝ｐ₁^ｌ₁＝３　・・・(24)
∴　ｎ＝２³・３＝２４　・・・(25)

以上(i)〜(iii)より、φ（ｎ）＝８を満たす自然数ｎは、
　　　ｎ＝１５，１６，２０，２４，３０　・・・（答）
である。

（２）φ(ｎ)＝２０＝２²×５　・・・(26)
(i)ｎ＝２^k（ｋは正の整数）のとき
　　　φ(ｎ)＝２^k-1　　（∵(1)より）
　　　　　　＝２²×５　・・・(5)
となり、矛盾する。

(ii)ｎ＝２ｌ＋１（ｌは正の整数）のとき
　　　φ(ｎ)＝２^mＳ₁Ｓ₂・・・Ｓ_m ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1・・・ ｐ_m^ｌ_m-1　（∵(4)より）
　　　　　　＝２²×５　・・・(27)
従って、１≦ｍ≦２でなければならない。

（ア）ｍ＝１のとき
　　　φ(ｎ)＝２Ｓ₁ｐ₁^ｌ₁-1＝２²×５
　　∴　Ｓ₁ｐ₁^ｌ₁-1＝２×５
　　∴　（Ｓ₁,ｐ₁^ｌ₁-1）＝（２，５）、（１０，１）　・・・(28)

(a)Ｓ₁＝２　かつ　ｐ₁^ｌ₁-1＝５のとき
　　　ｐ₁＝２Ｓ₁＋１＝５
となり、ｐ₁は奇素数になる。ｐ₁^ｌ₁-1＝５より、ｌ₁＝２
　　　ｎ＝ｐ₁^ｌ₁＝５²＝２５　・・・(29)

(b)Ｓ₁＝１０　かつ　ｐ₁^ｌ₁-1＝１のとき
　　　ｐ₁＝２Ｓ₁＋１＝２１
となり、ｐ₁が素数であることに矛盾する。

（イ）ｍ＝２のとき
　　　φ(ｎ)＝２²Ｓ₁Ｓ₂・ ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1 ＝２²×５
∴　Ｓ₁Ｓ₂・ ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1 ＝５ ・・・(30)
Ｓ₁＜Ｓ₂より、Ｓ₁＝１,Ｓ₂＝５　かつ ｌ₁＝ｌ₂＝１　・・・(31)
このとき、
ｐ₁＝２Ｓ₁＋１＝３
ｐ₂＝２Ｓ₂＋１＝１１
となり、ｐ₁、ｐ₂は奇素数になる。
∴　　ｎ＝ｐ₁^ｌ₁・ｐ₂^ｌ₂＝３×１１＝３３　・・・(32)

(iii)ｎ＝２^k（２ｌ＋１）（ｋ，ｌは正の整数）のとき
　　　φ(ｎ)＝φ（２^k）φ（２ｌ＋１）
　　　　　　＝２^k-1・φ（２ｌ＋１）
　　　　　　＝２²×５　・・・(33)

φ（２ｌ＋１）は、偶数だから、０≦ｋ−１≦１、すなわち、１≦ｋ≦２でなければならない。

（ア）ｋ＝１のとき
　　　φ（２ｌ＋１）＝２²×５　・・・(34)
(11)より、２ｌ＋１＝２５，３３　・・・(35)
∴　ｎ＝５０，６６　・・・(36)

（イ）ｋ＝２のとき
　　　φ（２ｌ＋１）＝２^mＳ₁Ｓ₂・・・Ｓ_m ｐ₁^ｌ₁-1・ｐ₂^ｌ₂-1・・・ ｐ_m^ｌ_m-1　（∵(4)より）
　　　　　　　　　　＝２×５　・・・(37)

従って、ｍ＝１でなければならない。

　　　φ（２ｌ＋１）＝２Ｓ₁ｐ₁^ｌ₁-1＝２×５
∴　　Ｓ₁ｐ₁^ｌ₁-1＝５
∴　　（Ｓ₁,ｐ₁^ｌ₁-1）＝（１，５）、（５，１）　・・・(38)

(a)Ｓ₁＝１　かつ　ｐ₁^ｌ₁-1＝５のとき
　　　ｐ₁＝２Ｓ₁＋１＝３
となり、３^ｌ₁-1＝５を満たすｌ₁は存在しないので矛盾する。
(b)Ｓ₁＝５　かつ　ｐ₁^ｌ₁-1＝１のとき
　　　ｐ₁＝２Ｓ₁＋１＝１１
となり、ｐ₁は奇素数となる。ｐ₁^ｌ₁-1＝１より、 ｌ₁＝１
∴　　２ｌ＋１＝ｐ₁^ｌ₁＝１１　・・・(39)
∴　　ｎ＝２²×１１＝４４　・・・(40)

以上(i)〜(iii)より、φ（ｎ）＝２０を満たす自然数ｎは、
　　　ｎ＝２５，３３，４４，５０，６６　・・・（答）
である。

問題２

（１）１００を素因数分解すると、

　　　１００＝２²×５²

となる。１から１００までの自然数のうち、２の倍数、５の倍数、１０の倍数の個数はそれぞれ５０個、２０個、１０個である。従って求める個数は、

　　　１００−（５０＋２０−１０）＝４０　・・・（答）

（別解）
求める個数は、φ（１００）である。
∴　　　φ（１００）＝φ（２²×５²）
　　　　　　　　　　＝φ（２²）φ（５²）
　　　　　　　　　　＝（２²−２）（５²−５）
　　　　　　　　　　＝４０　　　・・・（答）

（２）１から１００までの自然数のうち、２の倍数の和、５の倍数の和、１０の倍数の和をそれぞれ、 Ｓ₁、Ｓ₂、Ｓ₃とおくと、

である。１から１００までの自然数の和をＳとおくと、

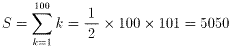
である。従って、求める数は、

　　　Ｓ−（Ｓ₁＋Ｓ₂−Ｓ₃）＝５０５０−（２５５０＋１０５０−５５０）
　　　　　　　　　　　　　　　＝２０００　　　・・・（答）

問題３
（３）
ｎ＝ｐ₁^ｌ₁ｐ₂^ｌ₂・・・ｐ_m^ｌ_m
（ｌ₁，ｌ₂，・・・，ｌ_mは正の整数； ｐ₁，ｐ₂，・・・，ｐ_mは素数； ｐ₁＜ｐ₂＜・・・＜ｐ_m）

と表すと、ｎの約数は、

　　　ｐ₁^α₁ｐ₂^α₂・・・ｐ_m^α_m
（０≦α₁≦ｌ₁，０≦α₂≦ｌ₂， ０≦α_m≦ｌ_m ；^α₁，^α₂，・・・，^α_mは整数）

と表せるので、求める数をNとおくと、

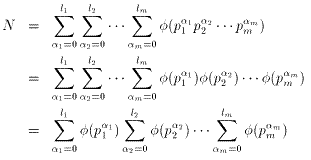
となる。また、

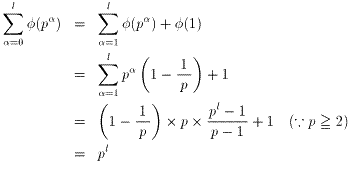
より、

　　　Ｎ＝ｐ₁^ｌ₁ｐ₂^ｌ₂・・・ｐ_m^ｌ_m＝ｎ　・・・（答）

問題３の（３）の結果から、求める数は、２０　・・・（答）

問題３の（３）の結果から、求める数は、１００　・・・（答）

NO.1549

2005.7.24.

水の流れ

不思議な平方根

第１５８回数学的な応募問題

皆さん、今年の大学入試を眺めていたら、東京大学で、こんな問題がでていました。これを問題にします。

問題１：３以上９９９９以下の奇数で、ａ^２−ａが１００００で割り切れるものをすべて求めよ。

そこで、こんな問題を考えました。

問題２：整数Ｎにおいて、正の平方根√Ｎが１桁の整数になり、Ｎの下１桁と同じになるＮを求めよ。

問題３：整数Ｎにおいて、正の平方根√Ｎが２桁の整数になり、Ｎの下２桁と同じになるＮを求めよ。

問題４：整数Ｎにおいて、正の平方根√Ｎが３桁の整数になり、Ｎの下３桁と同じになるＮを求めよ。

問題５：整数Ｎにおいて、正の平方根√Ｎが４桁の整数になり、Ｎの下４桁と同じになるＮを求めよ。

参考：　この整数Ｎを覚えていて、生徒が持っている計算機の画面に入力をします。下１，２、３，４桁を変えなでように画面のボタンをワンタッチで操作してください。どのボタンを操作したら良いでしょうか。

注）この記事に関する投稿の掲載は、８月１５日以降とします。

E-mail 戻る