| NO.1535 | 2005.5.3. | DDT | 何故πは3.141592・・・(3) |
Kernighanさん、ありがとうございます。目から鱗が落ちました。そうですよね、弧長表示を使っている限り、外部から与える計量との関係は出てきません。以下は、もしかすると無内容な内容をもってまわって述べているだけかもしれませんが、お付き合い頂ければ幸いです。
1.自然(?)標構
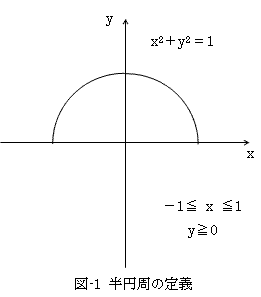
図-1にように半円周を定義します。ここで(x,y)座標を用いているのは単なる慣習によることで、 特に深い意味はありません。この半円周の長さを計算することを考えてみます。
半円周の長さを測るには、どうしたら一番簡単でしょう?。
半円周に糸を当てて、それを真っ直ぐに伸ばし、それに物差しを当てるのが最も簡単そうです。図-2-①~③にその様子を表します。
ここで物差しとは図-2-③のx軸の単位長さa = 1です。
さらに、図-2-③で、物差a = 1と半円周に沿った糸の長さbとを物理的に比較して比をとることが、長さの測定です。
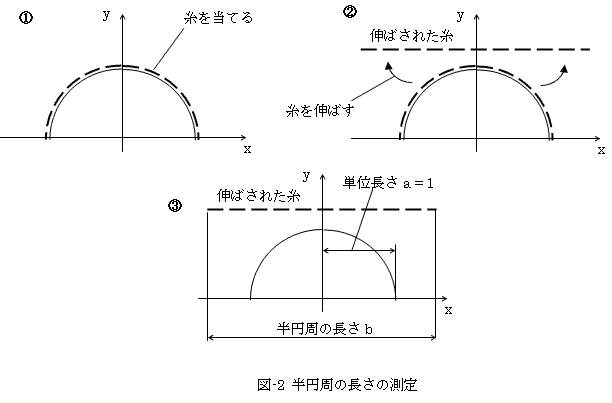
図-2-①と②にように、曲線も真っ直ぐに伸ばせば、直線であるx軸と同じです。実際これは、弧長表示の考え方の原型です。図形に沿った座標系を考えれば、曲線は直線と同じであり、曲面は平面と同じだというわけです。それは曲線上に、自然な座標系を導入することでもあります。
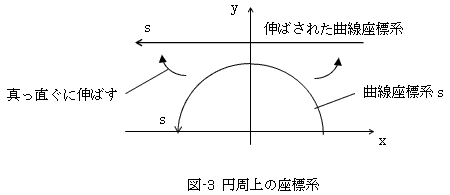
図-3にように自然(?)標構s(弧長表示と同じ)を定義してしまえば、半円周の長さを求めるのはひどく簡単に思えます。実際それは、x軸上で長さを計算するのと同じで自明であるはずです。
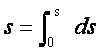 (1)
(1)
となります。(1)は、x軸上での次の積分(2)と全く同じ意味を持ちます。
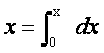 (2)
(2)
これが自然標構のすごさです。どんなに複雑に曲線が折れ曲がっていようと、それに沿った座標系では、長さの計算をx軸上と全く同じに行えます。ですが、sの具体的数値は、いくらでしょう?。
2.問題の定義
sの具体的数値は、いくらでしょう?。sには、任意の数値を与えられます(意外なことに?)。それが図-4です。実際、自然標構sの上下端には、任意の数値を当てられます。それは s = 0~1でも良いし、s = 0~πでも良いし、ことによったら s = 0~∞ でもかまいません。自然標構sとは、曲線のパラメータ表示の一種にすぎず、曲線のパラメータ表示のパラメータ区間には、どのような実数区間でも当てられます。それらは全て、少なくとも同相だからです。つまり、パラメータ区間上の点の順序を表す具体的な数値順序が、最初に方向づけた曲線の点の順序に合っていれば、どれでも採用できるからです。
しかし何か釈然としません。式(1)に対してそのようなことが起こるならば、式(2)に対しても同様な事態になるはずです。例えば図-5にように、x軸上に長さ2の直線を考えます。その直線にとっての自然標構とは、xそのものです。
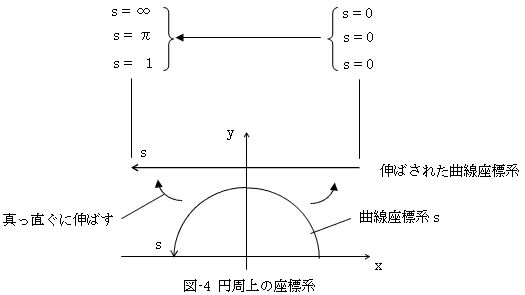
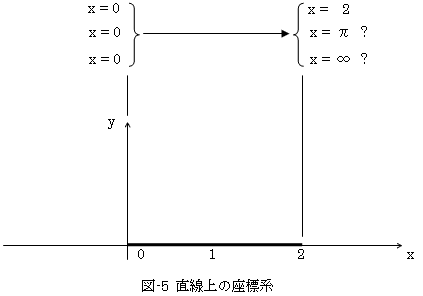
自然標構が、曲線のパラメータ表示の一種である以上、図-5にようにx = 0~2でも、x = 0~πでも、 x = 0~∞でも良いことになります。しかしx = 0~πや x = 0~∞とすることは可能ですが、やはり?がつきます。それは「x軸上の長さ2の直線」と最初からわかっているからです。何故わかったかといえば、x軸に計量が定義されているからです(x軸の目盛です!)。
一方、図-4において、sには目盛がありません。逆にs = 0~1やs = 0~πやs = 0~∞ とすることによって、それに整合する目盛を(計量を)定義したことになります。結局自然標構を導入するとは、次のことを意味します。
じつはこのことは、「距離関数の恣意性」としてNO.1118で知ったかぶりして書いたことでした。以下、NO.1118の一部です。
「メートル原器」が必要なのです。「メートル原器」という任意に決めた単位長さと、任意の長さとを比較することによって距離は決まります。ここで「メートル原器」の決め方は、全くの任意です。言いかえれば距離の単位はア・プリオリには決められず、もっと一般的に距離関数には無限の恣意性があります。距離関数の定義は次のようなものでした。
1.d(x,y)≧0,xとyはその間の距離を計ろうとする2点(← この意味はどうとでもとって下さい).
2.d(x,y)=0は、x=yに限られる.
3.d(x,y)+d(y,z)≧d(x,z)(三角不等式).
この制限を満たす限り、その間の距離を計ろうとする2点間の距離値には、任意の実数を当てて良いということになります。ただし距離関数の定義3.から、より遠い距離にはより大きな実数が当てられますが、そのような整合性を守る限り、距離関数(と距離値)には無限の恣意性があります。
田村祐三の「数学の哲学」によれば、距離を計るには二つの図形を重ねられる操作可能性が、必要と書かれています。リーマンもその就任公演で、同様の事を言ったと彼は書いています。
まったく知ったかぶりして書くもんじゃありません。その通りの事態が起こっています。図-5では実際に直線とx軸を物理的に比較して(目で見て目盛を読んで)長さを決めています。直線とx軸とは別物です。つまり直線の外部にあるx軸の計量を、直線の外から与えて長さを計っています。
では半円周の長さの計るとは、どのような問題でしょう?。
半円周の外部にあるx軸の計量を、半円周の外から与えて長さを計れ!
となるはずです。それが図-2です。x軸の単位長さの物差a = 1と、半円周に沿った糸の長さbとを物理的に比較して比をとることが、長さの測定です(リーマンの言ったとおりだ!)。よって式(1)の正しい計算方針は、
自然標構sを、外部座標xと関連付けて計算せよ!
となります。
3.半円周の長さを計算する
図-1より半円周は、x2+y2=1 かつy≧0なので、
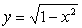
と表せます。線素dsは、
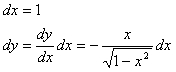
なので、
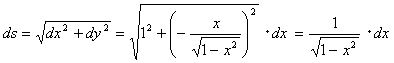
となります。従って、単位円の半円周の弧長であるπは、
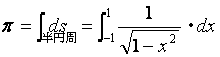 (3)
(3)
です。被積分関数である、
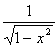 (4)
(4)
は、sin-1 xの1階導関数になっています。しかし思わず、
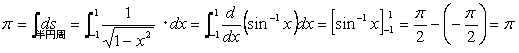 (5)
(5)
などとやってしまうと、もとの木阿弥です。πの具体的数値が知りたいなら、あくまで半円周に対する外部座標であるxのままで頑張る必要があります。(5)のようなスマートな書き換えは、今の場合不可です。
しかし(5)にも使い道がないわけではありません。目的は、積分(5)のxでの表現です。例えばsin-1 xのマクローリン展開を使う手があります。ただしsin-1 xのマクローリン展開の収束半径は |x|<1で、x = ±1では収束しません。積分(5)の積分区間の上下端±1では、被積分関数(4)の挙動が怪しくなるので、こうなってしまいます。でもここまで来れば、具体的な計算方針はもう明らかです。
πの値は、逆三角関数のマクローリン展開から計算できます(三角関数の意味を考えれば自明だった!)。逆三角関数のマクローリン展開というならば、何もsin-1 xを使う必要はありません。tan-1 xがあります。tan-1 xの収束半径は|x|≦1で、sin-1 xより遥かに扱いが容易です。
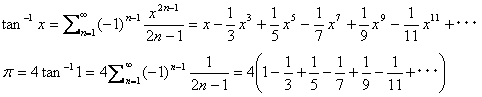
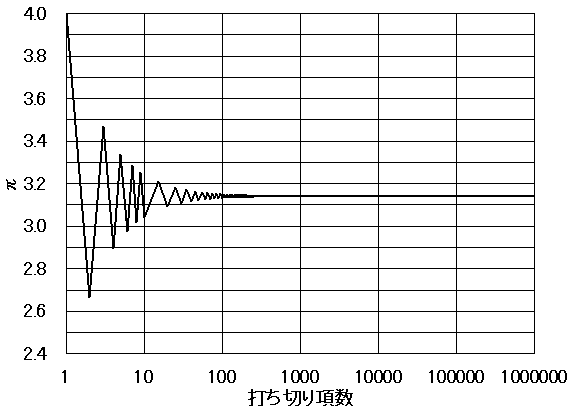
ちなみにExcelマクロで1,000,000項まで計算してみると、
π = 3.14159165358978
であり、同じExcelのWorkSheet PI( ) 関数では、
π = 3.14159265358979
となります。やっぱり収束半径の縁端なので収束が悪いです。
それにしても、この話を息子に説明するのには骨が折れそうです。

| NO.1536 | 2005.5.3. | 小学名探偵 | 選挙の結果 |
部員数が13人のクラブで部長と副部長を選挙で選ぶことになりました。5人が立候補しました。
選挙の際に、各投票者は投票者名をあかすことなく(無記名で)、2名に○を記入します。
○がついた数の一番多い立候補者が部長になり、二番目に多い立候補者が副部長になります。
結果は、
Aさんに○が1つ、
Bさんに○が3つ、
Cさんに○が5つ、
Dさんに○が7つ、
Eさんに○が10つきました。
(1)このような集計結果になるのは何通りありますか。
たとえば、下に示すのはそのうちの1通りです。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 1 | :AとDを選んだ人が一人 | |||
| 1 | 1 | :BとCを選んだ人が一人 | |||
| 1 | 1 | :BとDを選んだ人が一人 | |||
| 1 | 1 | :BとEを選んだ人が一人 | |||
| 4 | 4 | :CとEを選んだ人が四人 | |||
| 5 | 5 | :DとEを選んだ人が五人 |
(2)また、集計結果が
Aさんに○が1つ、
Bさんに○が2つ、
Cさんに○が6つ、
Dさんに○が7つ、
Eさんに○が10のとき、この結果になるのは何通りありますか。
(3)また、部員数が15人のランダムクラブの選挙では、5人の立候補者の誰にも○が6つ
ついてしまいました。この結果になるのは何通りありますか。

| NO.1537 | 2005.5.5. | 三角定規 | 何故πは3.141592・・・(4) |
NO.1535「何故 π=3.141592… (3)」は tan-1x のマクローリン展開を利用するもので,筆者 DDT さんご自身がおっしゃっておられるように,(高校生の)息子さんに説明するのは骨が折れそうです。そこで,円周を内接正多角形の周長で近似する素朴な方法を考えてみました。最終的には数列の極限を考えるので高校1年生にはまだ難しいかもしれませんが,2年生の秋頃にでも理解できるようになるのではないでしょうか。
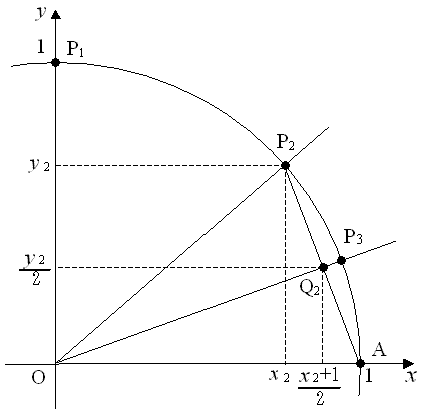
図のように半径1の第1象限の4分円弧 AP1 を次々に半分にしていきます。図は P3 まで描かれています。図において 線分 AP2 は正 8 角形の一辺(=L2 とします)で,これで円弧 AP2 を近似することにします。すなわち,n=2 の時点で 円周 2π≒8L2 とするのです。
このように進めれば,4分円弧 AP1 を n-1 回2等分して得られた線分 APn は正 2n+1 角形の一辺(=Ln )で,半円周 π≒2nLn と近似することができます。
さて,Pn の座標を定めるのに三角関数を用いてはいけないのですから,次のようにしました。
すなわち,線分APn の中点をQn とし,OQn の延長と円周との交点をPn+1 とします。
このようにすれば,Pn (xn,yn) 対し,
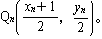
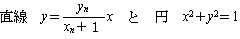
の交点を求めることで,
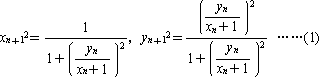
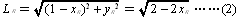
となります。
これらをもとにエクセルを用いて xn,yn,2nLn を逐次計算してみました。

これによればn=14 のときがπの近似値を小数点以下8桁まで正しく導いています。n=15以上で精度が悪くなるのは「丸め誤差」の増加のためと思われます。ここではエクセルの内部計算ルーチンをそのまま利用していますが,長い桁数を精密に計算するには計算方法の抜本的な検討が必要です。しかし,このことは息子さんの当初の疑問からは離れた別の問題でしょう。

| NO.1538 | 2005.5.7. | 水の流れ | 不思議な戦い方 |
皆さん、セ・パ交流試合を始めた今年のプロ野球はどう感じられますか。ジャイアンツファンの太郎さんは、ちっともおもしろくありません。こんな戦い方をしたらどうでしょうか。連続するどの3連戦の中にも勝ち○と負け●を少なくとも1試合作る戦い方です。すなわち、3連勝はないが、3連敗もしない戦い方です。
ここで、n試合行った結果、この不思議な戦い方で勝敗の起こる方法は何通りあるか考えてみます。
1試合経過のときは、○か●の2通りです。2試合経過のときは、○○か○●か●○か●●の4通りです。
問題1:3試合経過のときは何通りあるか。
問題2:4試合経過のときは何通りあるか。
問題3:n試合経過のときは何通りあるか。
補題:この数列は一般にどのような規則性がありますか。

| NO.1539 | 2005.5.14. | 佐野允信 | 不思議な戦い方(2) |
n試合経過したときに勝敗が起こる場合を考える。このとき、左から順に、1試合目からn試合目までの結果を1列に並べる。この列の数をanとする。n試合経過したときに勝敗が起こるのは次の4つの場合である。
(ア)(n-1)試合目が●、かつn試合目が○。
(イ)(n-2)試合目が●、かつ(n-1)試合目が○、かつn試合目が○。
(ウ)(n-1)試合目が○、かつn試合目が●。
(エ)(n-2)試合目が○、かつ(n-1)試合目が●、かつn試合目が●。
(ア)~(エ)の場合の数をそれぞれ、αn、βn、γn、δnとすると、
an=αn+βn+γn+δn ・・・(1)
と表せる。
(n+1)試合経過したときに勝敗が起こる場合の列は、n試合経過したときに勝敗が起こる場合の列の右端に、○または●をつけ加えることでつくればよい。
(i)n試合目が、●かつ(n+1)試合目が○の場合
(ウ)と(エ)の場合の列の右端に○をつけ加えればよいので、
αn+1=γn+δn ・・・(2)
(ii)(n-1)試合目が●かつn試合目が○かつ(n+1)試合目が○の場合
(ア)の場合の列の右端に○をつけ加えればよいので、
βn+1=αn ・・・(3)
(iii)n試合目が○かつ(n+1)試合目が●の場合
(ア)と(イ)の場合の列の右端に●をつけ加えればいいので
γn+1=αn+βn ・・・(4)
(iv)(n-1)試合目が○かつn試合目が●かつ(n+1)試合目が●の場合
(ウ)の場合の列の右端に●をつけ加えればいいので
δn+1=γn ・・・(5)
よって、
| an+1 | =αn+1+βn+1 +γn+1+δn+1 |
| =2αn+βn+2γn+δn (∵(2)~(5)より) ・・・(6) |
従って、
| an+2 | =αn+2+βn+2 +γn+2+δn+2 |
| =2αn+1+βn+1+2γn+1+δn+1 (∵(2)~(5)より) | |
| =2(γn+δn)+αn+2(αn+βn)+γn (∵(2)~(5)より) | |
| =3αn+2βn+3γn+2δn | |
| =an+1+an (∵(1),(6)より、nは3以上の自然数) ・・・(7) |
問1
○と●とを一列に並べる方法は23=8通りある。このうち、○○○と●●●の場合を除かなければならないので、求める方法の数は、8-2=6通りである。
問2
○と●とを一列に並べる方法は24=16通りある。このうち、次の場合を除かなければならない。
(1) ○または●が4個連続して並ぶ場合
この場合の数は、2通りである。
(2) ○または●が3個連続して並ぶ場合
この場合の数は、2×2=4通りである。
従って、求める方法の数は、16-(2+4)=10通りである。
問3
問1と問2より、すべての自然数nに対してan+2=an+1+anが成り立つ。
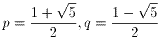
とおくと、
an+2-pan+1=q(an+1-pan) ・・・(8)
an+2-qan+1=p(an+1-qan) ・・・(9)
と表せる。よって、
an+1-pan=qn-1(a2-pa1) ・・・(10)
an+1-qan=pn-1(a2-qa1) ・・・(11)
(11)-(10)より、
(p-q)an=a2(pn-1-qn-1)-pqa1(pn-2-qn-2)
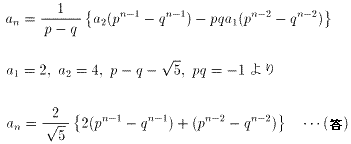

| NO.1540 | 2005.5.14. | 夜ふかしのつらいおじさん | 不思議な戦い方(3) |
n試合経過のときの場合の数をf(n)で表すことにします。
問題1:f(3)=6通り
問題2:f(4)=10通り
問題3:
f(n)=[(3+√5){(1+√5)/2}n-1+(3-√5){(1-√5)/2}n-1]/√5
補題:f(n+2)=f(n)+f(n+1)
f(1)は{○,●}の2通りです。
f(2)は{○○,○●,●○,●●}の4通りです。
f(3)は{○○●, ○●○,○●●, ●○○,●○●, ●●○}の6通りです。
f(4)は、
{○○●○,○○●●, ○●○○,○●○●, ○●●○,
●○○●, ●○●○,●○●●, ●●○○,●●○●}
の10通りです。
さて、k回目が勝ちの場合を書き出してみます。
勝ちや負けが3回続くことがないので、(k-1)、k、k+1、k+2回目の様子は、
次の2通りしかありません。
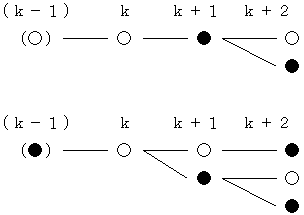
k+1回目とk+2回目で同じ勝敗の場合は1通りしかないので、k回目と同じ個数です。
残りのk+2回目はk+1回目と勝敗が必ず異なるので、k+1回目と必ず同じ個数あります。
また、k回目が負けの場合は、上の場合の勝敗がちょうど反転したものです。
だから、補題の解答が成立します。
f(n+2)=f(n)+f(n+1)
ところで、補題の漸化式は、適当な、α、βを選ぶと、
f(n+2)-βf(n+1)=α{f(n+1)-βf(n)}・・・・・①
と変形できます。(①はαとβに関して対称式です)
これは、{f(n+1)-βf(n)}が初項f(2)-βf(1)で公比がαの等比数列である
ことを示しています。
すると、
f(n+1)-βf(n)={f(2)-βf(1)}×αn-1・・・・・②
①が対称式なので、αとβを入れ換えた
f(n+1)-αf(n)={f(2)-αf(1)}×βn-1・・・・・③
も成立します。
よって、②、③を連立させると、
f(n)=[{f(2)-βf(1)}αn-1-{f(2)-αf(1)}βn-1]/(α-β)
このα、βは、x2=1+xより求められます。
解のx=(-1±√5)/2を適当にα、βとします。
また、f(1)=2、f(2)=4を代入すれば、
f(n)=[(3+√5){(1+√5)/2}n-1+(3-√5){(1-√5)/2}n-1]/√5

 E-mail
E-mail
 戻る
戻る