| NO.1464 |

| NO.1465 | 2004.6.5. | 松井 満 | 相加・相乗平均(2) |
問題1

問題2
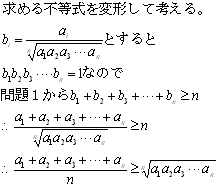

| NO.1466 | 2004.6.6. | 水の流れ | 素因数の積 |
太郎さんは平成15年2月25日には大阪大学の吹田キャンパスで前期の入試問題にチャレンジしていました。
今回は文系の問題を出題します。良く考えると裏にはオイラーが1734年に発見した事実が隠されていました。


| NO.1467 | 2004.6.13. | 松井 満 | 素因数の積(2) |

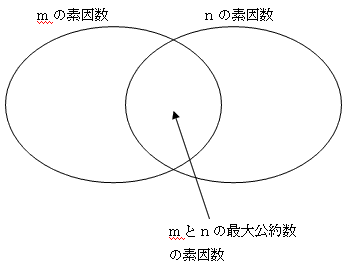
(2) (1)においてf(d)が1と2の場合を考えればよい。
| f(d)=1 | f(d)=2 | |
|---|---|---|
| m | n | n |
| 1 | 1,2,3,4,5,6,7,8,9,10 | |
| 2 | 1,3,5,7,9 | 2,4,6,8,10 |
| 3 | 1,2,4,5,7,8,10 | |
| 4 | 1,3,5,7,9 | 2,4,6,8,10 |
| 5 | 1,2,3,4,6,7,8,9 | |
| 6 | 1,5,7 | 2,4,8,10 |
| 7 | 1,2,3,4,5,6,8,9,10 | |
| 8 | 1,3,5,7,9 | 2,4,6,8,10 |
| 9 | 1,2,4,5,7,8,10 | |
| 10 | 1,3,7,9 | 2,4,6,8 |
| 合計 | 63 | 23 |
したがって
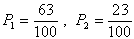

| NO.1468 | 2004.6.18. | yokodon | 等間隔の3点から z 軸を見ると? |
〜模試シリーズ18〜
xyz 空間に、条件
x = 1 , z < y
を満たす点 (x, y, z) の全体からなる不透明な半平面 π と、条件B:
x > 1, y > 0 , z = 0
を満たす点 (x, y, z) の全体からなる xy 平面上の領域Dがある。
3点A,B,Cは領域Dに含まれる点で、B (2, 1, 0) であり、この3点はこの
順に等間隔で xy 平面上の直線 l 上に並んでいるものとする。
3点A,B,Cから z 軸を見ると、半平面 π によって遮られて見えない部分と
見える部分とに分けられる。このとき、3点A,B,Cから見える z 軸の部分の z
座標の最小値が、それぞれ 2, 1, 1/2 であった。
直線 l の方程式を求めよ。

| NO.1469 | 2004.6.27. | 水の流れ | ある数列(1) |
太郎さんは、ある数列の問題を見つけました。考えてください。
「初項1,公比3の等比数列 1,3,9,27,81,243,729,・・・がある。
この数列から異なるいくつかの数をとってたしてできる数列を小さい順に並べてできる数列
1,3,4,9,10,12,13,・・・
を考えるとき、この数列の100番目はどんな数か。」

| NO.1470 | 2004.6.28. | 松井 満 | ある数列(2) |
初項1,公比3の等比数列から異なるいくつかの数をとってたしてできる数列を
小さい順に並べてできる数列を として、これを3進法で表すと下記のようになる。
| n | 3進法表示 | 10進法表示 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 10 | 3 |
| 3 | 11 | 4 |
| 4 | 100 | 9 |
| 5 | 101 | 10 |
異なる数ということから、3進法表示するときに0と1だけを使用することになる。
結局、上の表からわかるようにnを2進法で表し、 それをそのまま3進法に読みかえることによってこの数列が求まる。
したがってn=100のときは2進法で表すと1100100なので3進法に読みかえると
729+243+9=981となる。

 E-mail
E-mail
 戻る
戻る