コロキウム室

NO.127　　　　 7/4 　　水の流れ　　　 つり銭の問題（３）

問題の中で、500円玉を払うのをＡ，1000円玉を払うのをＢとします。 釣り銭がないので、常にａの数がｂの数より等しいか大きければよいのです。 これをａを→、ｂを↑と表せば、→がｎ個、 ↑ がｎ個を一列に並べる方法を考えます。

ここで、碁盤の目をした最短経路の問題に変化していきます。 分かり易くするために、求める数をＫ(n)とすると、 Ｋ(１)＝１，Ｋ(２)＝２，Ｋ(３)＝５は図を書いて、分かるとします。
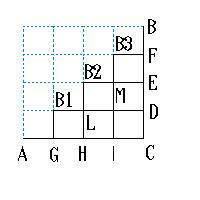
ｎ＝４のときを描きます。 図のような△ＡＢＣの最短経路の道筋がＫ(４)になります。

＜考え方からの副産物＞

Ｋ(４)を求めるのに、

1. Ｂ１を通るとき、Ａから Ｂ１を通り、△Ｂ１ＤＢの最短経路Ｋ(３)の道筋
2. Ｂ１を通らず、Ｂ2を通るとき、 △GHLの最短経路Ｋ(１)から、道路ＬＢ２を通り、 △Ｂ２ＥＢの最短経路Ｋ(２)の道筋
3. Ｂ１、Ｂ２を通らず、Ｂ３を通るとき、 △ＧＩＭの最短経路Ｋ(２)から、道路ＭＢ３を通り、 △Ｂ３ＦＢの最短経路Ｋ(１)の道筋
4. 最後に、Ｂ１，Ｂ２、Ｂ３を通らず、 Ｂに行く場合は△ＧＣＦの最短経路Ｋ(３)に等しい。

よって、Ｋ(４)＝ Ｋ(３)＋Ｋ(１)Ｋ(２)＋Ｋ(２)Ｋ(１)＋ Ｋ(３)
              ＝５＋１×２＋２×１＋５＝１４　になります。

また、こんな数え方（書き込み方式）もできます。

 
　　　            14Ｂ　
                  ↑             
              ５→14Ｆ          
              ↑  ↑
          ２→５→９Ｅ          
　　　　  ↑　↑  ↑
　　　１→２→３→４Ｄ          
      ↑  ↑  ↑  ↑
  Ａ→１→１→１→１Ｃ

さらに、斜めの線に関しての対称性に気がつけば、
Ｋ(４)＝ １×１＋３×３＋２×２＝１４
Ｋ(５)＝ １×１＋４×４＋５×５＝４２
Ｋ(６)＝ １×１＋５×５＋９×９＋５×５＝１３２
したがって、カタラン数Ｋ(ｎ)は何個かの平方数の和でできています。

さて、本題に入ります。ｎ＝４で描きます。

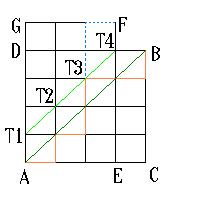
□ＤＡＣＢの最短経路の道筋は、階乗の記号を使えば、
（４＋４）！÷（４！×４！）＝７０　通り あります。
ここから、対角線ＡＢと交わる経路が不適ですから、 この不適な経路を求めます。
例えば、図の太線の経路は不適ですが、 これを直線Ｔ１Ｔ４について対称移動します。
ただし、直線Ｔ１Ｔ４に始めて出会った点から 後の部分のみを対称に曲げて図の太い波線を考えると、 全ての不適な経路は□ＡＥＦＧの最短経路の数に等しくなります。
これは、 （５＋３）！÷（５！×３！）＝５６　通りとなり、 求めるカタラン数Ｋ(４)は、
Ｋ(４) ＝_８Ｃ_４−_８Ｃ_３ ＝７０−５６＝１４　になります。
一般に、
Ｋ(ｎ) ＝_２ｎＣ_ｎ −_２ｎＣ_ｎ−１ ＝_２ｎＣ_ｎ÷（ｎ＋１） となります。

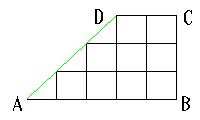
そこで、また、問題です。 次の台形ＡＢＣＤの最短経路は何通りありますか。

　

NO.128　　　　 7/8 　　水の流れ　　　 ジョギングの問題（１）

私は日曜日の朝、いつの９ｋｍの道のりをジョギングしています。 出発点で時速６ｋｍ、到着点では時速３ｋｍに減少していて、 健康のために、いつも途中の時速は、歩いた距離の１次関数となる ようにしています。私のジョギング時間は果たして何時間でしょう。

NO.129　　　　 7/12 　　Junko　　　　 ジョギングの問題（２）