Weekend Mathematics/コロキウム室/NO.169
| NO.1402 | 2003.7.6. | 水の流れ | 増えた1cm2(1) |
太郎さんは、月曜日第7限の「総合的な学習の時間」に1年生を対象にして、「楽しい数学」と称した講座を受け持っています。現在は「フィボナッチ数列」の調べ学習をしています。この中で、次のような課題を生徒に伝えています。皆さんも、考えて、増えた1cm2 はどうしてか 考えてください。
参考:{an}:{1,1,2,3,5,8,13,21,34,55,89,・・・}をフィボナッチ数列という。
問題:
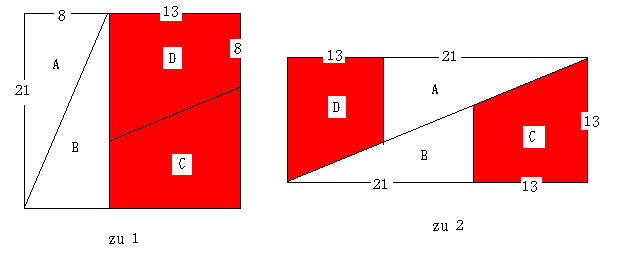
最初 1辺が21cmの正方形を下の図のように4つの部分に分けました。三角形Aと三角形Bは合同、三角形Cと三角形Dは合同です。次に、この4つを移動させて、[zu2]の図形を作りました。 見た目は長方形ですから、面積を考えてみると、横13cm、縦(13+21)cmになります。 4つの部分を移動しただけですから、面積は同じになるはずです。どうして、1cm2違うのでしょうか。この違いは、「フィボナッチ数列」にどんな性質があるからでしょうか。


| NO.1403 | 2003.7.12. | teki | 増えた1cm2(2) |
この問題は、古くからある有名なパズルで、21×21cmの正方形を4つに切
って並べ替えると、実は中央にほんの少しの平行四辺形の形をした隙間(この面積が
1cm2)ができるんです。
ここまでは、知っているのですが、これとフィボナッチ数列との関係にはびっく
りしました。
図に登場する、8、13、21という数字は、全てフィボナッチ数列にある数字
ですが、こうして分割した場合、最初の1が残るということなんでしょうね。
つまり、一見直線に見える長方形の対角線(?)は、実は直線ではなく、間に1
だけ平行四辺形の隙間ができるということなんでしょう。
要するに、フィボナッチ数列の中にある数字同士のわり算を実行した場合、
どの2つの数字をとっても、その比が全て異なるっていうことですね。

| NO.1404 | 2003.7.13. | Idaho Potato | 増えた1cm2(3) |
「増えた1cm2」の問題について、きちんとした解答はどなたか別の 方にお任せして、私からは与太話を少々…
《 1 》 塾講師のアルバイトをしていた頃、これより2項手前の「8x8 と 5x13」で、実際 にボール紙を切ったものを並べて、中学生と高校生に「手品」として披露したこ とがあります。 正方形に並べるときに、わざと少し雑に並べて隙間を作るのがコツです(^^)。
《 2 》
それで、手品の種明かしをした後で、『並べ替えたときにできる「隙間」の鋭角
部分の角度を求めよ』と出題すると、高校生向けの手頃な練習問題になります。
近似計算なら、三角関数を用いなくても普通の電卓で計算できます。
上述の「8x8 と 5x13」の場合で計算すると約1.24度、本題の「21x21 と 13x34」
では約0.18度になります。
《 3 》
最後に少しまじめな話。
正方形の辺の長さを1、長方形の長辺と短辺の長さをそれぞれ sqrt(5)+1 / 2, sqrt(5)-1
/ 2 (黄金比とその逆数)にして、同様の分割・並べ替えを行うと、隙間なくぴったり合わさります。
当然、面積は両方とも1で一致しています。
フィボナッチ数列の隣接3項の場合は、面積の過不足は必ず±1になるので、項を
進めていくと、「隙間」(または「重なり」)の全体に対する面積比は0に収束
します。
上述の黄金比を用いた正方形と長方形の組は、ちょうど、フィボナッチ数列の隣
接3項による正方形と長方形の組の「極限」になっているわけです。

| NO.1405 | 2003.7.26. | 水の流れ | フィボナッチ数列 |
太郎さんは、月曜日第7限の「総合的な学習の時間」に1年生を対象にして、「楽しい数学」と称した講座を受け持っています。現在は「フィボナッチ数列」の調べ学習をしています。この中で、次のような性質があるのではないかと生徒に伝えています。 参考:{an}:{1,1,2,3,5,8,13,21,34,55,89,・・・}をフィボナッチ数列という。


 E-mail
E-mail
 戻る
戻る