Weekend Mathematics/コロキウム室/NO.168
コロキウム室
| NO.1399
| 2003.6.15. | 水の流れ | 5乗根・10乗根
|
第121回数学的な応募問題
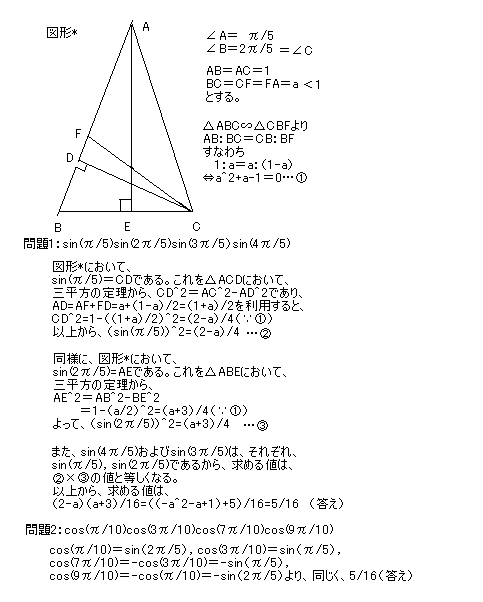
今回は、1の5乗根や10乗根に関係の深い3角関数の積の問題です。


| NO.1400
| 2003.6.16. | ひろぽん | 5乗根・10乗根(2)
|

| NO.1401
| 2003.6.18. | yokodon | 三角関数の和
|
〜模試体験S号外〜
n を 2 以上の自然数とする。
- ある n-1 次多項式 Pn(x) と n 次多項式 Qn(x) が存在して、全ての実数θに対して、
sin(2nθ) = n・sin(2θ)・Pn(sin2θ), cos(2nθ) = Qn(sin2θ)
・・・を満たすことを証明せよ。
- αk =1/ sin2(kπ/2n) , k = 1, 2,..., n-1
・・・とおくと、次式が成り立つことを示せ。
Pn(x) = (1- α1・x)(1- α2・x)×...×(1- αn-1・x)
- 2.の αk に関して、次式が成り立つことを証明せよ。
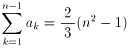

 E-mail
E-mail
 戻る
戻る





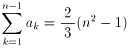

 E-mail
E-mail
 戻る
戻る