
Weekend Mathematics/コロキウム室/1998.1〜6/NO.16
NO.119 6/7 Junko 円に関する微分(7)
最初の例では、微分する変数と他の値が独立しています。
長方形の1辺と他の1辺、円柱では高さと底面の半径です。
ところが最後の円錐だけはだめです。
高さと底面積が独立変数ではないからです。

NO.120 6/9 ヴァー 円に関する微分(8)
その通りです。
つまり、底面積が高さの関数になっているということです。
S=S(h)ということです。
そのためV=Sh/3をhで微分すると、積の微分法を用いることで、
dV/dh = S/3 + (dS/dh)×(h/3)
になります。dV/dhが常にSであるためには、
dS/dh = 2S/h でなくてはなりません。
この式は常微分方程式で変数分離法で解けるものです。
実際に解いて見ると、S∝(hの2乗)になります。
これは相似比の2乗が面積比であるということを
意味しています。

NO.121 6/19 水の流れ つり銭の問題(1)
生徒が教材費に五百円払う必要があります。
そこに、五百円玉を 持ったn人の生徒と、
千円札しか持っていないn人の合計2n人の
クラス生徒がいます。
担任の私はつり銭を準備していませんでした。
つり銭が不足しないように生徒からもらう方法は
全部で何通りありますか。
ただし、生徒の2n人に区別しないで、
お金の出し方で考えてください。

NO.122 6/20 ぷー 円に関する微分(9)
微分の意味がよくわかってなかった、
とつくづく思いました。
定義を考えれば当然でした。
半径がrの円の面積を考える。
それと中心を同じくして半径がr+hの円を考える
その二つの円の面積の差は帯状の部分である。
f(r)=πr2とすると、
微分の定義は
lim(h→0) { f(r+h)-f(r)}/h はまさしく微分ですものね。
帯状の面積を考えて、hをかぎりなくちいさくすれば、
たしかにその面積の差は円周に近づいて行くんですよね。
だから円の面積を微分すると円周になる!
同じように球状の体積ではその体積の差は
表面積に近づいて行くんですね。
なんてすごいんでしょう。
微分万歳!!!

NO.123 6/20 水の流れ サ−ビス券の問題(4)
さて、サービス券の最後にいっておいた商品券のことです。
10000円の商品を買った場合、5000円の商品券がもらえます。
このことは、なるほど、10000円払ったうち5000円が戻って
くるのだから、半額だ、と直感的に誰でもそう思います。
しかし、本当に半額といえるでしょうか。
まず、10000円で品物Aを買い、5000円の商品券をもらいます。
その商品券で期間外に品物Bを買いにいきます。
払った金額は初めの10000円で、
買った品物はA,Bのあわせて15000円分です。
よって、割引率は5000÷15000≒33%となり、
おやおや、50offとはならないのです。
また、期間中に商品券5000円券で品物Bを買い、
ここで、戻ってきた商品券2500円券で品物Cを買い・・・
というふうに無限に(1円未満は考えない)続けていくと、
10000+5000+2500+1250+・・・=10000{1÷(1-1/2)}=20000(円)
で、本当に半額になるのでは。
でも、こんなことお店の人に言ったら、
どういわれるでしょうね。考えてみたことありますか。

NO.124 6/21 Junko つり銭の問題(2)
千円札を受け取る前に、
おつりになる五百円玉を持っていればいいのですね。
具体的に数え上げてみることにします。
500円玉をA、千円札をBと表記することにします。

NO.125 6/21 ヴァー 4桁の問題(3)
水の流れさんの「4桁の問題」に出て来る「並び替えて最大になるものから最小になるものを引く」ということばを関数だとおもって、この関数の振舞を図にしてみました。(だから、何なんだ。といわれたらそれまでなんですが...)
まずは、2桁の場合です。
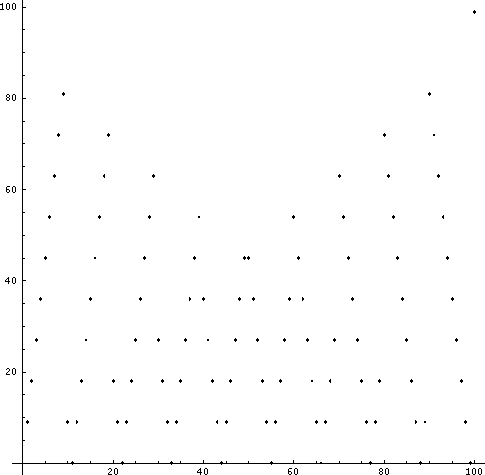
3桁の場合。
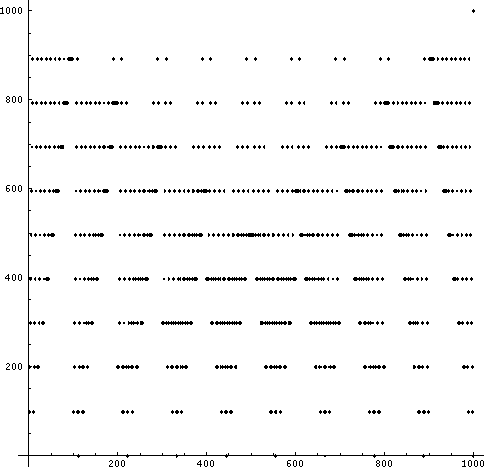
4桁の場合。
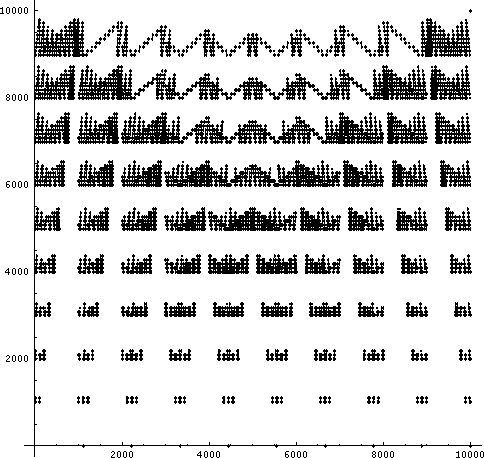
5桁の場合。点が大きすぎるからちょっと苦しい;-)
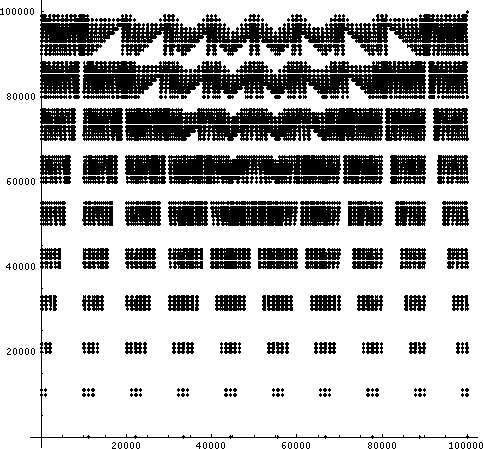
これらの図はもしかしたらフラクタルになってるのかなぁとも思えますが、そこまでは調べてません。ただ、予想がつくのは次のことです。
「中央に対して対称性がある」
もっと数学的な言い方をすると、
この関数をFとして、Fの定義域={0,1,2,3,...,10n-1}、つまり桁数がn-1以下の数全体とすると、
F(0)=F(10n-1),
F(1)=F(10n-2),
F(2)=F(10n-3),....
一般的には、
F(i)=F(10n-i-1)
(ただし、iは0から10n-1の間の自然数)
が成り立つということです。
証明はまだ出来てませんが、必ず成り立つと思います。

NO.126 6/26 Idaho Potato 円に関する微分(10)
高校数学だと、原始関数から積分を導入するので、 どうしても「定積分=区分求積法」の概念をとらえにくくなりますね。 (おまけに「微積分学の基本定理」のありがたみが分からなくなる。) 区分求積法の概念ができていれば、 「円周を積分→円の面積」「球の表面積を積分→球の体積」 が成り立つことは、すっきり理解できると思います。
塾でアルバイトをしていたときの話ですが、
高校生の生徒に、「積分の記法の成り立ち」を
次のように話したら、
それこそ「目から鱗」という表情で、驚いていました。
f(x) のグラフの下の領域の面積を求めたい。 そこで、その領域を短冊状に細かく切って、 短冊の面積を考えます。いかがでしょうか? こういう説明を受けると、 積分の後ろの「dx」がどういう意味か、 正しく理解できるようになるのではないでしょうか
まず、短冊の縦の長さは f(x) です。 横の長さは、x軸の「切れはし」のようなもの。 これを dx で表しましょう。 すると、1つの短冊の面積は f(x)dx となります。 それらの短冊の面積を「合計」したものが、求める面積です。 「合計」は英語で sum だから、頭文字の S をとって、 短冊の面積の「合計」を S f(x)dx で表しましょう。
そして、(ここからがちょっと苦しいのですが…) 真の面積に近づけるために、短冊の横幅を限りなく細くします。 そこで、「短冊の横幅を細くする」という気持ちを表すために、 先頭の S を「細く」書くと、∫f(x)dx となるのです!

 E-mail
E-mail
 戻る
戻る