コロキウム室

ガウスの発散公式を利用した、任意多角形の面積，重心，慣性ﾓｰﾒﾝﾄの計算法です。

１．面積
例えば右図の領域R（滑らかな太線）の面積を計算する手順です。Rの境界Sの表式がわかっている場合でも、それを折れ線近似して（R内部の細い実線として）扱ったほうが、計算が速くて便利だったりするので、以後任意多角形の場合のみ扱います。もちろん図-1は、もう数倍細かく近似したほうが良いです。

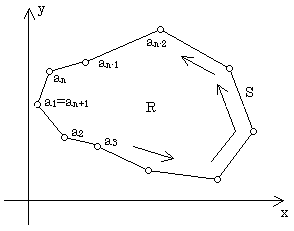図-2の任意多角形に対して、その角点を、左回りの順番にa₁，a₂，･･･，a_nとします。a₁は、どこから始めようとOKです。また出発点a₁は1周して元に戻った時、a_iの添数iが、nから１に突然ｼﾞｬﾝﾌﾟしないように、a₁＝a_n+1と二重化しておくと便利です。
図-2の任意多角形Rの面積に関する通常の考えでは、Rの境界Sをy方向の高さに関して2つの関数、y＝h₁(x)とy＝h₂(x)に分け、その差（h₂(x)−h₁(x)）をxで積分することによって計算するか、または多角形領域Rを三角形分割して、部分三角形の面積の合計として算出します。しかしこれらの方法では、面積は形から決まるという至極当然の事実が、直截には使われていません。

面積Aは、NO.1320で述べたように、

　　

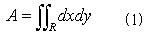
で計算できます。一方ガウスの発散公式（発散定理）は、

　　

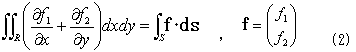
でした。式(1)，(2)の意味は申し訳ないですがNO.1320を見てください。式(2)の右辺の線積分は、積分領域Rの境界Sなので、左辺の2重積分が境界曲線Sの形から直接決まることを示します。よって、もし式(1)の右辺の2重積分が(2)の左辺に等しいなら、面積Aが境界曲線Sの形から直接決まることになります。式(1)の右辺＝式(2)の左辺とは、

　　

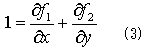
を意味します。そこで(3)を成り立たせる2変数関数f₁(x，y)とf₂(x，y)を探します。(3)を満たせばf₁とf₂は何でも良いので、

　　

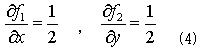
とします。ここから、

　　

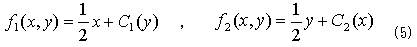
がただちに出ます。ここでC₁とC₂は、y，xに関する1回微分可能な任意の関数です。再び(3)さえ満たせば良いことから、C₁＝C₂＝0でもOKなので、

　　

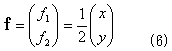
と決めます。明らかに(6)の決め方には、任意性がありますが、ここでは(x，y)について対称なものを選びました。面積という量は、座標系の取り方によって癖があってはいけないので、たとえ結果は同じであっても、(x，y)について対称な表式を選択するのが、妥当と思えます。
fの形が決まったので、図-2で定義した多角形の角点a_iの座標から、(2)の右辺を算出する計算にかかります。角点a_iの座標は多角形の形を定めるので、この情報だけから面積を計算できるはずです。
角点a_iからa_i+1への辺上では、

　　

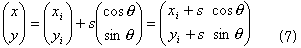
と書けます。ここでa_i＝(x_i，y_i)^T，a_i+1＝(x_i+1，y_i+1)^T，sは、　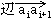　に沿った座標系，(cosθ，sinθ)^Tは、　　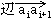の単位接線ベクトルで明らかに、

　　

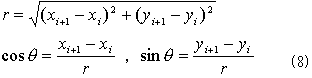
で計算できます。外法線線素ベクトルは、(8)のθを右にπ/2回した方向なので、

　　

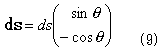
となり、(7)，(8)，(9)を式(2)右辺に代入すれ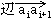ば、　　では、

　　

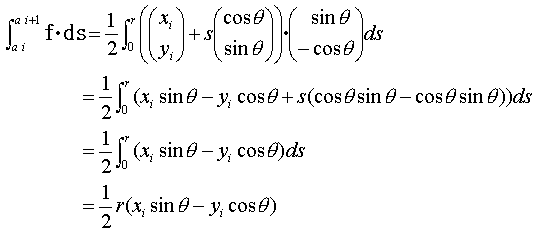
となり、式(8)を考慮すれば、

　　

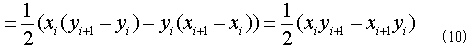
となります。これが多角形の1辺上での式(2)右辺の値なので、式(2)右辺全体としては（境界S全体では）、これらを寄せ集めて、

　　

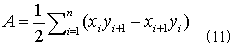
（後で気づきましたが、原点を中心に多角形領域を3角形分割した場合の、部分三角形の符号付面積の合計です。・・・当たり前の結果でした・・・）

が得られます。

２．重心位置
任意の領域Rの重心座標(x₀，y₀)は、NO.1320より、

　　

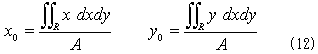
で計算できます。面積Aは、すでに１．でやっつけているので、右辺分子が計算できればOKです。x方向の重心座標x₀についての計算は、１．と同様に、

　　

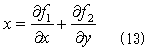
となるf₁(x，y)とf₂(x，y)を探します。ここでも(x，y)に関して対称になるように、

　　

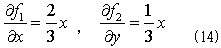
を採用します。式(4)から(5)を得たのと同じ発想で、

　　

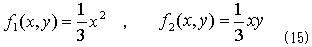
で十分です。よって、

　　

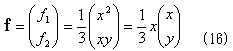
となりますが、式(16)のどこが(x，y)について対称なのでしょう？。まずこれは、x方向の重心位置を計算する式なので、x方向への偏りがなければなければなりません。それが式(16)最右辺のﾍﾞｸﾄﾙの係数xです。そしてﾍﾞｸﾄﾙの中身は１．のfに等しく、(x，y) について同じ式で構成されるので対称です。式(7)と(9)より、

　　

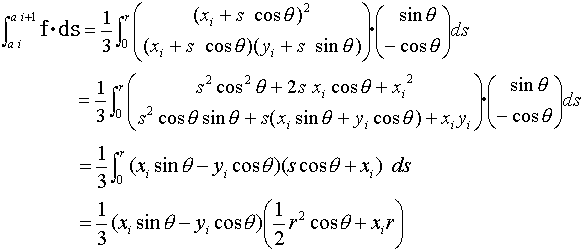
であり、式(8)を考慮すると、

　　

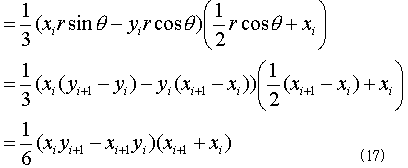
従って、

　　

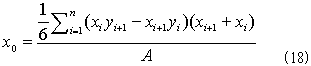
（さっきの部分三角形の重心の、面積の重み付き平均です。・・・知ってる人には、当たり前の結果でした・・・）

となります。y₀に関しては、最初の座標系を右にπ/2回転させれば、古い座標系のy軸を新しいx'軸とでき、x軸 → −y'軸，y軸 → x'軸の関係があるので、x → −y，y → xの交換を行えば、

　　

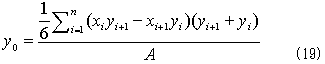
となります。

３．慣性ﾓｰﾒﾝﾄ
慣性ﾓｰﾒﾝﾄはふつう、重心まわりで計算されますが、任意の点(x₀，y₀)を中心としても同じです。

　　

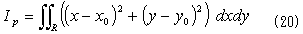
式(20)は、極断面2次ﾓｰﾒﾝﾄといわれる一種の断面係数で、物体の面密度一定なら、これに面密度ρをかけたものが慣性ﾓｰﾒﾝﾄです。回転中心(x₀，y₀)を原点とする座標系に移ります。

　　

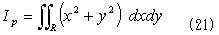
x²＋y²は最初から、(x，y)について対称性を持っているので、

　　

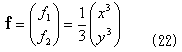
と決めます。

　　

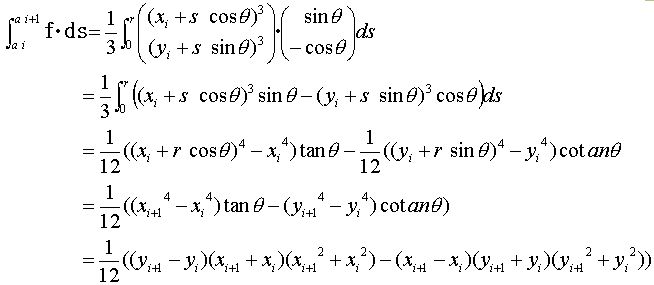
なので、

　　

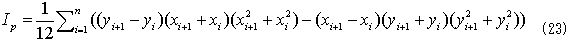
です。cosθ＝0の場合や、sinθ＝0の場合の場合分けをやっていないので少々反則気味ですが、場合分けしてやっても結果は変わりません。さらにこの(x，y)は、Ipの回転中心を原点とした座標系です。式(23)も幾何学的に解釈できますが、複雑になります。工学屋の発想としては、領域境界の座標を押さえれば各種量を計算できるということだけが重要です。ここでは都合良く工学屋に徹します。

E-mail 戻る