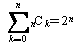
でも、この式を見ていて次のようなことを思い浮かびませんか?
そう、以下のような式も何らかの形で表せないかと。
Weekend Mathematics/コロキウム室/NO.150
| NO.1268 | 2002.9.7. | 中川 幸一 | relative expression of Permutation |
以前から考えていた問題なのですが、なかなか面白い問題ですので紹介しようと思い
ます。
2項係数の関係式で以下のような有名な関係式があることは良く知られています。
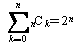
でも、この式を見ていて次のようなことを思い浮かびませんか?
そう、以下のような式も何らかの形で表せないかと。
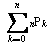
でも、これは岩波の公式集や色々なものを見ても載ってないんです。
CとPを入れ替えただけですから、これなら昔の人が考えていてもおかしくないはずですが・・・。
(昔は順列Permutationの記号Pはなかったから一概にはいえませんが。)
そこでこの式の一般化を考えてみました。
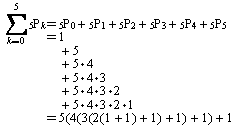
以上のことから帰納的に以下のような数列を求めることに帰着できました。
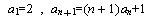

| NO.1269 | 2002.9.7. | 中川 幸一 | ぞろ目(4) |
UBASICで友達とプログラムを考えて実行させて見ました。
プログラムの中身は以下のようになっています。
list 10 'save "ぞろ目" 20 cls 3 30 dim M(4) 40 for I=0 to 4 50 read M(I) 60 next I 70 print "0を入力すると終了します。" 80 print "" 90 input "桁は";X:if X=0 then end 100 for P=2 to X 110 for I=0 to 4 120 A=M(I)*(10^P-1)*2 130 N=int(sqrt(A/9)) 140 if A-N*(N+1)*9=0 then print N,(A/9)/2 150 next I 160 next P 170 print "" 180 goto 90 190 data 1,3,5,6,8

| NO.1270 | 2002.9.7. | BossF | 2直線上の動点の距離(2) |
いい問題だと思います
[解]
t=0 における、Pの位置をA、Qの位置をB
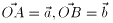
また、l,m のP,Qの進行方向向きの方向ベクトルを
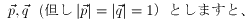
題意より
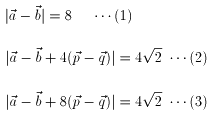
ここで、さらに
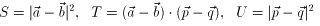
としますと
(1)より S=64
(2)より S+8T+16U=32
(3)より S+16T+64U=32
これを解いて
(S,T,U)=(64,-6,1) …(4)
さて、
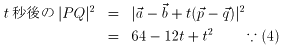
ですから、t=6 でPQは Min √28 すなわち 2√7(修正9/9、22:00)
また、U=1 より、l、mは、60°の角をなしています。■

| NO.1271 | 2002.9.7. | BossF | ぞろ目(5) |
「ぞろ目の四角数は存在しない」ことを、
wasmathさんのヒント
を補題の形で示した上で、
示そうと思います。
以下文字は、自然数とします。
補題1 奇数の平方≡1 (mod8)
[略証]
(2n-1)2=4n(n-1)+1
ここで、n(n-1) は偶数だから (2n-1)2≡1 (mod8) ■
補題2 m2=10n-1 を満たすm,n は m=3,n=1 に限る。
[略証]
10n-1=999…9 だから、m の一の位は、3か7
m=10k+3 とすると、m2=100k2+60k+9
よって、m2の十の位≡6k (mod10)
ところが、6kは偶数だから十の位は9にならない。
m=10k+7 の時も同様で
m2の十の位≡14k (mod10)だから十の位は9にならない。■
さて本題
まず、平方数の一の位は、0〜9を、平方することにより
容易に 0、1、4、5、6、9
したがって、補題2に注意すれば、ぞろ目としては、1、4、5、6を考えれば十分です。
m=2k の時 m2≡0 (mod4) ですから、平方数になるためには
m2の下二桁≡0 (mod4) が必要です。
ところが、66≡2 (mod4) で不適
また、m2=4k2=444…4 なら、両辺を4で割って
k2=111…1 ですから、
結局、ぞろ目として、1、5 を考えれば十分です。
すると、m;odd 必要です。
ここで、一般にN≡Nの下三桁 (mod8) です
ところが
11/≡1、111/≡1、55/≡1、555/≡1(mod8)
(/≡;合同でない)ですから、補題1より、1と5のぞろ目の平方数は存在しません。 ■
良く考えると、9≡1、99/≡1、999/≡1 (mod8) ですから、
補題2は特に示す必要はありませんね…(^^;;
これを中川君のぞろ目に使えないか考えてみましたが、だめみたいですね〜

| NO.1272 | 2002.9.7. | BossF | 三角形の内接円の半径 |
wasmathさんのHPのもうひとつの問題も、面白かったので、解いてみました
「周の長さが一定である三角形の内接円の半径が最大となるのは, 正三角形のときであることを示せ。」
[解]
三辺の長さをa,b,c a+b+c=2s としますと、半周より一辺は小さいから
s-a,s-b,s-c は正数ですので相加相乗平均の関係より
(s-a)(s-b)(s-c)≦[(s-a)+(s-b)+(s-c)}/3]3=s3/27
よって、ヘロンの公式より面積Sは、s-a=s-b=s-c i.e. a=b=c の時最大です。
ところで、内接円の半径を r とすれば、S=rs
したがって題意は示されました。 ■

| NO.1273 | 2002.9.8. | 浜田 明巳 | tanθの値を求めよ(1) |
前回の独り言に引き続き,気になっている問題をひとつ.
「(sinθ+cosθ)/(sinθ−cosθ)=2………(1) のとき,tanθの値を求めよ.」という問題をこのように解きました.
(sinθ+cosθ)/(sinθ−cosθ)=2の分母を払うと,
sinθ+cosθ=2(sinθ−cosθ)
∴sinθ=3cosθ………(2)
ここで,cosθ=0とすると,sinθ=3cosθ=0
これは,1=sin2θ+cos2θ=0となり,矛盾する.
∴cosθ≠0
(2)の両辺をcosθ(≠0)で割ると,
sinθ/cosθ=tanθ=3………(答)
これで勿論正解なのですが,私の気になっている点はここです.問題文で「tanθの値を求めよ」となっている事から,tanθの値は存在する事が分かる.だから,必然的にcosθ≠0となるのだから,わざわざcosθ≠0を求める必要はないのではないか,というものです.
「tanθの値を求めよ」という問題は,「tanθの値が存在する事を示し,かつそのときのtanθの値を求める」事まで要求するのか,という疑問です.
こういう事も考えられます.もしtanθの値が存在しない場合もあり得るのであれば,問題そのものが間違っているのであるから,つまり答が存在するという仮定が間違っているのであるから,結論は何でもかまわないはず.何を答えてもかまわないはずだから,わざわざtanθが存在するかどうかのチェックまでは必要ない.
慣習的には,上の解答通り,tanθの値が存在する事を示すべきでしょう.
私は,ここら辺の事をごまかし,sinθ=3cosθから,
tanθ=sinθ/cosθ=3cosθ/cosθ=3
と指導しました.こうすると,はじめからtanθが存在するのだから,cosθ≠0うんぬんは必要なし,という事で,一切授業ではふれませんでした.このごまかしはうまくいったと思います.
皆さんはどうお思いでしょうか.数学的にはどうなのでしょうか.

| NO.1274 | 2002.9.9. | yokodon | tanθの値を求めよ(2) |
今回の問題の件( (sinθ + cosθ)/(sinθ - cosθ) = 2 …[*] を満たす tanθ
の値)ですが、以下のようにすればスッキリ解決するのではないでしょうか。
もし、cosθ = 0 ならば sinθ = ±1 であり(複号任意)、([*] 式の左辺)
= 1 となって等式を満たしません。よって cosθ ≠ 0 であり(まぁ、ここまでは
背理法でしょうか)、[*] 式左辺の分母と分子を cosθ で割って、以下を得ます。
(tanθ + 1)/(tanθ - 1) = 2
これを tanθ について解けば、結論の tanθ = 3 を得ます。
満たす tanθ の値が存在しなければ、方程式が解なしである場合と似たような状
況なのだと思います。
有限の値を実際にとる事を示し、その値を求めるという方針で良いと思うのですが
、如何でしょうか。

| NO.1275 | 2002.9.9. | wasmath | tanθの値を求めよ(3) |
発言者がおっしゃる 『問題文で「tanθの値を求めよ」となっている事から,
tanθの値は存在する事が分かる 』 というのは誤りと言わざるを得ません。 問題文が
「tanθが存在するとき,(sinθ+cosθ)/(sinθ−cosθ)=2 となる必要条件を求めよ」
とでもなっているならともかくとして, 原問題文のままならば
「(sinθ+cosθ)/(sinθ−cosθ)=2を満たすtanθの値を求めよ」
と(同値変形を要求していると)解釈するのがふつうです。つまり,(論理的には)
「条件を満たす値が存在しない」が答にもなり得るということです。
存在をチェックしないで議論すると,思わぬ矛盾が生じることがあるので,乱暴に扱うわけにはいきません。例えば,
自然数の最大値をNとすると,Nの最大性よりN2≦Nであり,N>0であるからN≦1.
したがって,自然数は1しかない?
ただ, cosθ≠0を「示さなければいけないもの」ととらえるのではなく,「もしcosθ=0なら割れないのだからまず調べてみる」と自然に考えたいものです。それと同様に,両辺にsinθ−cosθをかけた時点で同値性が崩れていることも注意したいものです。sinθ≠cosθをどこかでチェックしておくべきでしょう。
本問に限って述べるならば,まず分母・分子をcosθで割ってtanθだけの式にする方が,目標がはっきりして考えやすいのではないでしょうか。また,「cosθで割るのだから0にならないかを確かめる」こともより自然に感じられます。 そのあとも, tanθ+1=0とtanθ-1=0は同時には成り立たないので,分母を払うときの注意も容易に乗り越えられると思います。
数学を学んだ人のすべてが研究者になるわけではないのですから,結果の数値を予測するといった直感よりも,何が正しく,何が間違っているのかを判断・理解することの方が大事だと私は考えます。

| NO.1276 | 2002.9.9. | BossF | tanθの値を求めよ(4) |
設問がいつも正しいとは限らないので、吟味した方がいいと思います。
まず第一に「解なし」も立派な解であること
第二に、めったにないことですが、入試問題でも、不適切な設問がなされることがありますので。

| NO.1277 | 2002.9.10. | 中川 幸一 | relative expression of Permutation(2) |
Mathematicaで計算をしてみた結果以下のようになりました。


 E-mail
E-mail
 戻る
戻る