
Weekend Mathematics/コロキウム室/NO.145
| NO.1239 | 2002.7.26. | BossF | 数列の一般項(2) |
まず、与えられた条件により f(n) は一意に決まることに注意する。…①
さて、g(n)=(n+1)/n とすると、
g(1)=2
また
| 1/g(n) + 2/(n+1) | =n/(n+1)+2/(n+1) |
| =(n+2)/(n+1) | |
| =g(n+1) |
基本的には帰納法と同じようなものですが考え方は
条件を満たす解は一つしかない→一つ条件を満たすものがある→それが解だ
という流れです。
私が現役の頃の経験で言えば、普通に帰納法で書くよりも1割がた書く量を減らせま
す。(^o^)

| NO.1240 | 2002.7.27. | 中川 幸一 | ルジャンドル多項式 (2) |
ルジャンドル多項式のグラフを一部図示してみました。
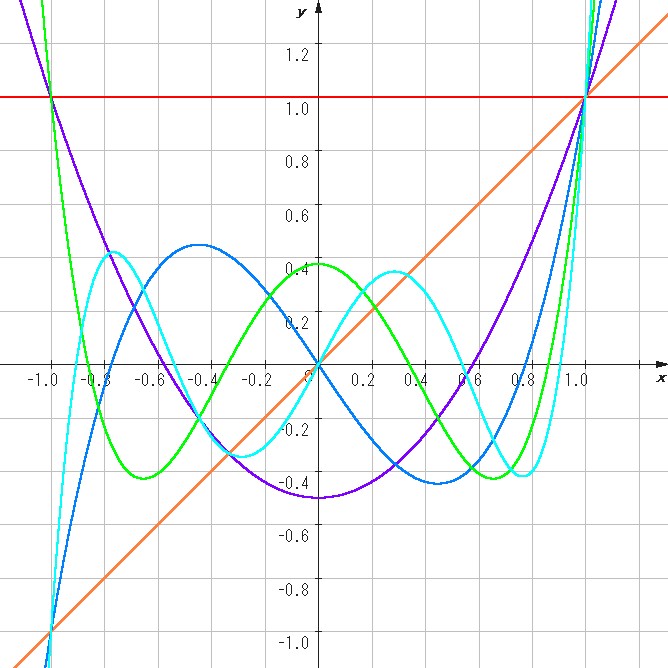
参考程度に並べておくと、
| n=0 | y=1 |
| n=1 | y=x |
| n=2 | y=(1/2)(3x2-1) |
| n=3 | y=(1/2)(5x2-3x) |
| n=4 | y=(1/8)(35x4-30x2+3) |
| n=5 | y=(1/8)(65x5-70x3+15x) |

| NO.1241 | 2002.7.27. | おいたん | マイナスとマイナスをかけるとプラス |
非常に基本的な質問で恐縮ですが….
マイナスとマイナスをかけるとプラスになることをわかりやすく説明するにはどうしたらよいでしょうか。

| NO.1242 | 2002.7.27. | BossF | マイナスとマイナスをかけるとプラス(2) |
たぶん、中学生相手の話だと思いますので、そのつもりで話します
-2x5=-10
は、-2が5個だよで、なっとくさせられるとおもいます。さらに
-2x4=-8
-2x3=-6
-2x2=-4
と書き出して、規則性に注意させて、続けて
-2x1=
-2x0=
-2x(-1)=
-2x(-2)=
を問題にすると、大抵の子は直感的に理解してくれます。

| NO.1243 | 2002.7.30. | 中川 幸一 | ぞろ目 |
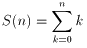
とおくとき、S(n)の値がぞろ目(ex.7777)となるnを求めよ!
以前この問題を考えていたのですが、桁数が2桁以上となるのは、
S(10) = 55
S(11) = 66
S(36) = 666
の3つしか見つかりませんでした。
他に解はあるのでしょうか?
これ以上ないならばない証明を教えてください。

 E-mail
E-mail
 戻る
戻る