Weekend Mathematics/コロキウム室/NO.142
| NO.1211 | 2002.5.7. | 夜ふかしのつらいおじさん | 相加相乗平均不等式(2) |
僕が知っている数学的帰納法による説明を紹介します。
まず、K=2のときは省略します。
次に、K=2kの場合です。
これは、原理的な説明で理解してもらえると思います。
例えば、k=3のときは、(K=8)

つまり、2つの場合をk重に使えばできます。
これでいくらでも大きな数(2k
の形)で成立することがいえました。
次に、Kで成立するとします。つまり、
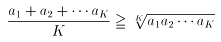
ここで、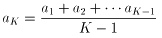 とおきます。
とおきます。
(K-1)個の相加平均とおくのです。そこで左辺を整理すると、
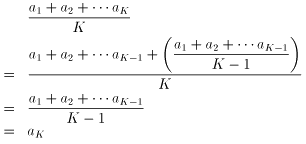
これと右辺とを比較して
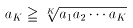
両辺をK乗すると
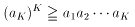
aK を約すと
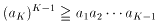
そこで両辺の(K-1)乗根をとると
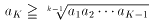
aK は(K-1)個の相加平均とおいているので1つ小さい値で成立します。これ
を繰り返して2kー1と2k の間を埋めることができるので説明ができたこと
になります。

| NO.1212 | 2002.5.9. | おっくん | 循環小数(1) |
有理数で疑問に思うことなんですが、よければ返答くださいませ!!
疑問点
小数で表示したとき、周期が5となる有理数と一般に周期がn(∞)
となる有理数は存在するのでしょうか??

| NO.1213 | 2002.5.9. | Junko | 循環小数(2) |
周期が5の無限小数については、適当に5桁の数(ただし5桁とも同じ数字はだめ)
を99999で割ればできると思います。
仮に、0<a<1で、周期5の循環小数「a=0.ABCDEABCDEABCDE・・・・」を考えます。
桁数を5桁ずらすために100000倍したものから、元の数aを引きます。
| 100000× | a= | ABCDE. | ABCDEABCDEABCDE・・・ |
| a= | 0. | ABCDEABCDEABCDE・・・ | |
| 99999× | a= | ABCDE |
a=ABCDE/99999
可能ならば約分をしてください。
同様に、周期nの無限小数も作ることができます。
n桁の数(これ自身が周期的なものはだめです。)を999・・・999(n個)で
割ればOKです。可能ならば約分をしてください。
周期が∞の無限小数というのは、周期が存在しないということですから、無理数とい
うことになるのではないかと思います。

| NO.1214 | 2002.5.14. | BossF | 正96角形(3) |
[補題]
半径1の円に内接する正n角形の1辺が a ならば、
半径1の円に内接する正2n角形の1辺は
(1+a/2)1/2-(1-a/2)1/2
[証明]
半径1の円O に内接する正n角形Nの各頂点に
Oから半径を下ろすとNはn個の二等辺三角形に分割され
そのひとつを、△OABとし、
OからABに下ろした垂線の足をH
更に、OHと、円Oの交点をMとすると
三平方より
OM={1-a2/4}1/2
したがって、
だから
HM2 =[1-{1-a2/4}1/2]2 =2-a2/4+2{1-a2/4}1/2
AM =(AH2+HM2)1/2 =[a2/4+2-a2/4+2{1-a2/4}1/2]1/2 ={2-2(1-a2/4)1/2}1/2 =(1+a/2)1/2-(1-a/2)1/2 ■
[問い1]~[問い4]
半径1の円に内接する正6角形の1辺は1だから
補題より
正12角形の一辺は(61/2-21/2)/2
以下同様なので略
[問い5]
補題の証明に用いた△OABで考える
∠AOB=2π/n だから
∠AOH=π/n
∴AB=2AH=2sin(π/n) …答
[問い6]
問い5より、半径1の円に内接する正n角形の周L は
L=2nsin(π/n)=2π x {sin(π/n)}/(π/n)
ここで n→∞ の時 π/n→0 だから、{sin(π/n)}/(π/n)→1
よって L→2π …答

| NO.1215 | 2002.5.15. | yokodon | 相加相乗平均不等式(3) |
一部修正 5/19 10:00
前回、後回しにした“log(x) の凸性”を用いる証明をご紹介します。
3段階に分けますね。
(1)凸関数に関する定理
区間 [a, b] 上で以下の不等式を満たす連続関数 f を凸関数といいます
(流儀によって符号が違う場合もありますが、ここでは xy 平面上で上に凸なグラフを描く場
合を考えます)。
f(a(1-t)+bt) ≧ (1-t)・f(a) + t・f(b) ・・・[1]
但し 0 ≦ t ≦ 1 であり、等号は t = 0, 1 の時のみ成り立つ。
ここで、関数 f が [a, b] 上で2回微分可能で、且つ同区間上にて f'' < 0 の
とき [1] が成り立つことを示すことが出来ます。その証明は、
F(t) =([1] の左辺)-([1] の右辺)
とおいて、
(2)log(x) が凸関数であること
{log(x)}'' = -1/x2 ですから、log(x) が(1)の凸関数の条件を満たすことは
明らかです。
(3)不等式の証明
ここで、2以上の自然数 n に関して、相加相乗平均不等式が成り立つことを示す
準備が出来ました。
n = 2 の場合は、[1] で f(x) = log(x) として
a = a1 、b = a2 、t = 1/2
におけば主張は成り立ちます(等号成立は a = b の場合のみ)。
n = m で求める不等式が成り立つとすると、
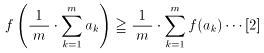
ここで、[1] において
a = am+1 、
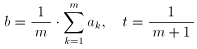
にとると、[1] の左辺の f の引数が
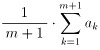
になることに注意して、
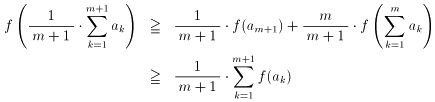
を得ます(第2の不等式は帰納法の仮定 [2] から)。
これから、n = m+1 でも求め
る不等式が成り立つことが言えます(等号成立条件は、やはり a = b から帰納的に
全ての ak , k =1,2,...,m+1 が等しい場合のみ)。
よって、数学的帰納法から、主張は成り立ちます。

| NO.1216 | 2002.5.18. | 水の流れ | 一列に手をつなぐ(1) |
太郎さんは前日、「地球に優しく」という環境をテーマにしたテレビ番組を観ていると、
何人かの人々が一列に手をつないでいる光景をみました。
大勢の人ですから、途中で先に何人かの人が手をつないで、
次に左隣りの人と手をつないでから、右隣りの一列のグループと手をつないでいました。
ここで、n人が一列に手をつなぐ方法が知りたくなりました。人は区別しません。
例えば、1人ですと、当然相手がいませんが、便宜的に1通りとしましょう。
2人だと、1-2とつなぎますから、これも1通りです。
3人だと、1-2とつないで3とつなぐ場合と、2-3と先につないだ後、
左から1とつなぐ場合がありますから、計2通りあります。
ここで、問題です。ただし、人と人が手をつなぐ場合は2人として、
同時に3人以上は考えないでください。
問1.n=4のとき、手をつなぐ順序は何通りか。
問2.n=5のとき、手をつなぐ順序は何通りか。
問3.一般に、n人のとき、手をつなぐ順序は何通りか。

| NO.1217 | 2002.5.21. | 月の光 | 開平方(1) |
整数の平方根を電卓でなく手で計算したいのですが、やり方を忘れてし
まったので教えていただけないでしょうか。

| NO.1218 | 2002.5.22. | BossF | 開平方(2) |
とても,メールでは,かけない(私の能力では…)ので、
紹介されているページを検索しました。
開平計算のやり方(PDF)
開平は高校で習ったんですが,そのとき一緒に、開立も習ったと思うんですが(本で
読んだのかも・・)こちらはすっかり忘れてしまいました。ご存知の方がいらっしゃっ
いましたら、お教えださい。

| NO.1219 | 2002.5.23. | 水の流れ | 一列に手をつなぐ(2) |
一部解釈の違いで異なる解答が出ています。
混乱を招く不手際をお許しください。今から修正します。
だから、こう解釈したから、この答えになるというものでもかまいません。
作問者の意図は「同時に二人またはグループで手をつなぐ組があった場合は1つと考えてください。
例えば 4人のとき (1-2)-(3-4)とつなぐ場合は1つと数えてください。」

| NO.1220 | 2002.5.25. | BossF | 一列に手をつなぐ(3) |
n人が、手をつなぐ順序を f(n) とする
(i)f(1)=1
(ii)n≧2 の時
最後には、必ず、二つのグループの端同士が手をつなぐから、
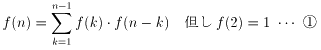
①はカタラン数であることを示す
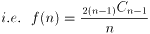 …②
…②
②式は n=1 でも成立
よって一般にn人の時
手をつなぐ順序は,
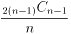 通り ■
通り ■

 E-mail
E-mail
 戻る
戻る