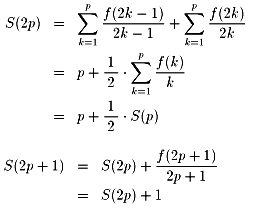
傛偭偰戣堄偼帵偝傟偨仭
Weekend Mathematics乛僐儘僉僂儉幒乛NO.125
| NO.1064 | 2001.10.11. | BossF | 慺場悢暘夝傪堦晹梡偄偰掕媊偝傟傞悢楍乮俀乯 |
1丏傑偢 n=b丒2a 側傜丄2n=b丒2a+1偩偐傜丄
f(2n)=f(n) i.e. {f(n)/n}/2=f(2n)/(2n)乧嘆
傑偨丄f(2n+1)=2n+1偩偐傜丄f(2n+1)/(2n+1)=1乧嘇
偱偁傞偙偲偵拲堄偡傞丅
嘆嘇傛傝
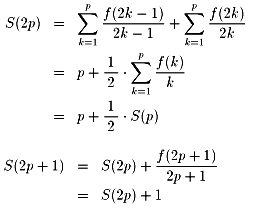
傛偭偰戣堄偼帵偝傟偨仭
2丏梌偊傜傟偨慟壔幃傪夝偔偙偲偵傛傝 a(j)=2j-1
偙偙偱丄S(1)=1偵拲堄偟偰丄
S(2p)=S(p)/2+p傪孞傝曉偟梡偄傞偙偲偵傛傝
| S(2n) | =1/2(1/2(乧1/2(1/2(1/2S(1)+1)+2)+4)乧)+2n-2)+2n-1 |
| =1/2n +1/2n-1+2/2n-2+22/2+乧+2n-2/2+2n-1 | |
| =1/2n +1/2n-1{1+22+24+乧22(n-2)}+2n-1 | |
| =1/2n +1/2n-1[{(22)n-1-1}/(22-1)]+2n-1 | |
| =乧=2n+1/3+1/(3丒2n) |
| 亪S(aj) | =S(2j-1)-f(2j)/2j |
| =2j+1/3+1/(3丒2j)-1/2j | |
| =2/3丒(2j-2-j)乧摎 |
PS偦偺俀丏栤戣暥偵倐偑婏悢偱偁傞偙偲傪柧婰偟偨傎偆偑偄偄偱偡偹丏
椺偊偽侾俀亖俀倶俇亖俀俀倶俁偱偳偪傜傪偲傞偐偼丄柧帵偝傟偰傑偣傫丅

| NO.1065 | 2001.10.17. | yokodon | 慺場悢暘夝傪堦晹梡偄偰掕媊偝傟傞悢楍乮俁乯 |
an 偺堦斒崁偵娭偟偰偼丄慟壔幃偐傜 an 亖 2n - 1 丅
傑偨丄an 偺慟壔幃偲乮1乯偺寢壥偐傜丄
| S(an+1) | 亖 S(2an + 1) |
| 亖 S(2an) + 1 | |
| 亖 1/2丒S(an) + an + 1 |

| NO.1066 | 2001.10.17. | yokodon | 惓嶰妏宍偺撪晹傪摦偔慄暘乮侾乯 |
柾帋僔儕乕僘6
a 偼 併3亙 a 亙 2 傪枮偨偡掕悢偲偡傞丅
堦曈偺挿偝偑俀偺惓嶰妏宍俙俛俠偺曈俙俛丄曈俙俠忋乮扐偟丄抂揰傪彍偔乯偵偦傟
偧傟揰俹丄揰俻偑偁傝丄俹俻亖 a 傪枮偨偟側偑傜摦偔傕偺偲偡傞丅
嶰妏宍俙俹俻偺柺愊偺庢傝偆傞抣偺斖埻傪丄a 傪梡偄偰昞偣丅

| NO.1067 | 2001.10.18. | BossF | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俀乯 |
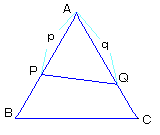
AP=p , AQ=q 偲偍偔丄
傑偢梋尫掕棟傛傝丂
a2=p2+q2-2pq丒cos60亱=p2+q2-pq
亪(p-q)2+pq=a2, i.e. pq=a2-(p-q)2
偟偨偑偭偰丂pq亝a2
傑偨丂p or q 仺0 偱丂pq仺0 偼偁偒傜偐
傛偭偰丂0亙pq亝a2
偝偰
仮APQ=pq丒sin60亱x1/2=乮併3/4乯pq偩偐傜
仮APQ亝乮併3/4乯a2 (摍崋偼AP=AQ偺帪)乧摎

| NO.1068 | 2001.10.19. | 悈偺棳傟 | 嬌戝抣偲嬌彫抣偺嵎乮侾乯 |
崱丄懢榊偝傫偼妛峑偱旝暘朄丒愊暘朄傪嫵偊偰偄傑偡丅
巊梡偟偰偄傞曗彆嫵嵽偺拞偵偙傫側栤戣偑偁傝傑偟偨丅
乽倶偺俁師娭悢丂倖(倶)亖倎倶俁亄倐倶俀亄們倶亄倓丂乮倎亜侽乯
偑倶亖兛偱嬌戝抣傪偲傝丄倶亖兝偱嬌彫抣傪傕偮偲偒丄嬌戝抣偲嬌彫抣偺嵎傪兛丄兝偱昞偣丅乿
栤戣侾丏摫娭悢倖亴(倶)亖侽偑堎側傞俀偮偺幚悢夝傪帩偪丄
偦偺夝偑兛丄兝偱偁傞偙偲傪棙梡偟偰夝偄偰偔偩偝偄丅
栤戣俀丏娭悢倖(倶)傪旝暘偡傞偲丄倖亴(倶)偱偡偑丄媡偵丄
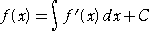
偱偁傞偙偲傪棙梡偟偰傕夝偗傑偡丅

| NO.1069 | 2001.10.21. | 傗側偣 | 杺朄恮乮係乯 |
杺曽恮僨乕僞儀乕僗
傪尒偰傒傞偲
婏悢偺杺朄恮偼magic偲揷怷曽幃偲摨堦偺傾儖僑儕僘儉丒丒
傓偭傓偮偐偟偄乣乣側傫偨傜偐傫偨傜偱偡偑
偦偺夝摎傪尒偰偄傞偆偪偵桳傞朄懃乮偙傟傪傾儖僑儕僘儉偭偰偐丠乯傪
敪尒偟傑偟偨丅
| 17 | 23 | 4 | 10 | 11 |
| 24 | 5 | 6 | 12 | 18 |
| 1 | 7 | 13 | 19 | 25 |
| 8 | 14 | 20 | 21 | 2 |
| 15 | 16 | 22 | 3 | 9 |
俆儅僗偺杺朄恮偱愢柧偟傑偡丅
傑偢侾偺埵抲偱偡偑丄嵍抂偺楍偺恀傫拞
俀偼偦偺斀懳懁嫶偺楍偱侾傛傝堦抜偟偨偺強
偙偙傑偱偼婏悢儅僗栚偺杺朄恮側傜偳傟傕摨偠偱偡丅
師偺俁偐傜偱偡偑丄俀偐傜幬傔嵍壓偵抂傑偱弴師乭俁乭悢帤傪擖傟偰偄偒傑偡丅
乮偄偗側偄応崌丄彙栚偑俁偺帪偩偗偼丄堦斣忋偺楍偱俀偺埵抲傛傝
堦偮偩偗嵍懁傊乯
堦斣壓偺抜傑偱峴偭偨傜丄師偺悢帤乭係乭偼堦斣忋偺抜偺乭俁乭傛傝堦偮偩偗嵍偵
偦偙偐傜嵍幬傔壓偵楢懕偟偨嬻儅僗傪弴師杽傔偰偄偒傑偡丅
仏嵍抂傑偱擖傞偲偒偼偦偺傑傑偱丄搑拞偱嬻儅僗偑愗傟偨応崌偼乮崱夞偼乭俆乭傪擖
傟偨抜奒偱
乭侾乭偵摉偨傞偺偱乯偦偙偐傜塃偺埵抲傊堦屄偩偗堏摦偟偰乭俇乭傪擖傟傑偡
偦偙偐傜枖嵍幬傔壓傊弴師悢帤傪擖傟傑偡丅
嵍抂傑偱擖偭偨偲偒偼丄乭侾乭偲乭俀乭偺帪偺傛偆偵塃抂偱慜偺悢帤傛傝堦抜偟偨偺
強偵
偙偺帪偵嵍堦斣壓偵峴偭偨偲偒偼丄師偺悢帤偼塃懁偵
師偺悢帤偼丄傑偨偟偰傕堦斣忋偺堦偮嵍懁傊丄偙傟偺孞傝曉偟偱
婏悢偺杺朄恮偼夝偗傑偡丅僗儔僗儔偲彂偒崬傫偱偄偗偽偐偭偙偄偄偱偡傛偹
彈偺巕儌僥儌僥偵側偭偨傝偟偰丄傕偆庤抶傟偐乮敋徫乯
偦偺忋偵偙傟偺忋壓丄嵍塃斀懳偺搝傕墳梡偡傟偽丄
巹偑慜偵憲偭偨夝摎偲堦晹廳暋偡傞偐傕偟傟傑偣傫偑
摨偠彙栚偺婏悢杺朄恮偱傕俉庬椶偺夝摎偑丒丒丒
壗偐愢柧晄懌偱嵪傒傑偣傫丅帺暘偱偼擺摼偟偰嫃傞傫偱偡偑乮徫乯
偪側傒偵偙偺俫俹偵偁傞俈偺杺朄恮傪暲傋偰偍偒傑偡
| 30 | 38 | 46 | 5 | 13 | 21 | 22 |
| 39 | 47 | 6 | 14 | 15 | 23 | 31 |
| 48 | 7 | 8 | 16 | 24 | 32 | 40 |
| 1 | 9 | 17 | 25 | 33 | 41 | 49 |
| 10 | 18 | 26 | 34 | 42 | 43 | 2 |
| 19 | 27 | 35 | 36 | 44 | 3 | 11 |
| 28 | 29 | 37 | 45 | 4 | 12 | 20 |

| NO.1070 | 2001.10.21. | BossF | 嬌戝抣偲嬌彫抣偺嵎乮俀乯 |
栤戣1
f 乫(x)=3ax2+2bx+c乧嘆 偱偁傞偐傜丄
夝偲學悢偺娭學傛傝
兛+兝=-2b/3a,兛兝=c/3a乧嘇
偝偰
| f(兛)-f(兝) | |
| = | a(兛3-兝3)+b(兛2-兝2)+c(兛-兝) |
| = | a(兛-兝){兛2+兛兝+兝2+(b/a)(兛+兝)+(c/a)} |
| = | a(兛-兝){兛2+兛兝+兝2+(-3/2)(兛+兝)2+3兛兝}(佹嘇) |
| = | (a/2)(兝-兛)3 乧摎 |
栤戣俀
[夝]
傑偢堦斒偵
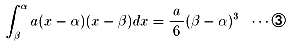
偱偁傞偙偲偵拲堄偡傞丅
偝偰
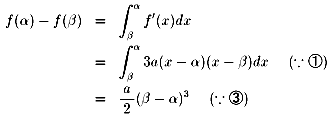

| NO.1071 | 2001.10.22. | 昹揷丂柧枻 | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俁乯 |
俙俹亖倶丆俙俻亖倷偲偡傞丏
仮俙俹俻偵偍偄偰丆梋尫掕棟偐傜丆
俹俻2亖俙俹2亄俙俻2亅俀丒俙俹丒俙俻丒cos佢俹俙俻
亪倎2亖倶2亄倷2亅倶倷乧乧乧(1)
偙偺曽掱幃偱昞偝傟傞僌儔僼傪丆尨揰傪拞怱偵偟偰兤夞揮偝偣傞丏
偙偺夞揮傪昞偡幃偼丆
丂丂倶'亖倶cos兤亅倷sin兤丆倷'亖倶sin兤亄倷cos兤
偱偁傞偐傜丆
丂丂倶亖倶'cos兤亄倷'sin兤丆倷亖亅倶'sin兤亄倷'cos兤
偲側傞丏
(1)偵戙擖偡傞偲丆
丂丂倎2亖(倶'cos兤亄倷'sin兤)2亄(亅倶'sin兤亄倷'cos兤)2亅(倶'cos兤亄倷'sin兤)(亅倶'sin兤亄倷'cos兤)
丂丂亪倶'2(侾亄sin俀兤乛俀)亄倷'2(侾亅sin俀兤乛俀)亅倶'倷'cos俀兤亖倎2
cos俀兤亖侽偲偡傞堊偵偼丆兤亖兾乛係偲偡傟偽傛偄丏
偙偺偲偒丆
丂丂俁倶'2乛俀亄倷'2乛俀亖倎2
丂丂亪倶'2乛(俀倎2乛俁)亄倷'2乛(俀倎2)亖侾
丂(倶'丆倷')傪(倶丆倷)偵偐偊傞偲丆
丂丂倶2乛(俀倎2乛俁)亄倷2乛(俀倎2)亖侾乧乧乧(2)
偙傟傪昞偡僌儔僼偼恾侾偱偁傞丏
恾侾
偮傑傝(1)偺昞偡僌儔僼偼丆恾侾偺僌儔僼傪尨揰傪拞怱偵偟偰亅兾乛係夞揮偟偨傕偺偺丆
倶亜侽丆倷亜侽偺晹暘偱偁傞丏偮傑傝恾俀偲側傞丏
恾俀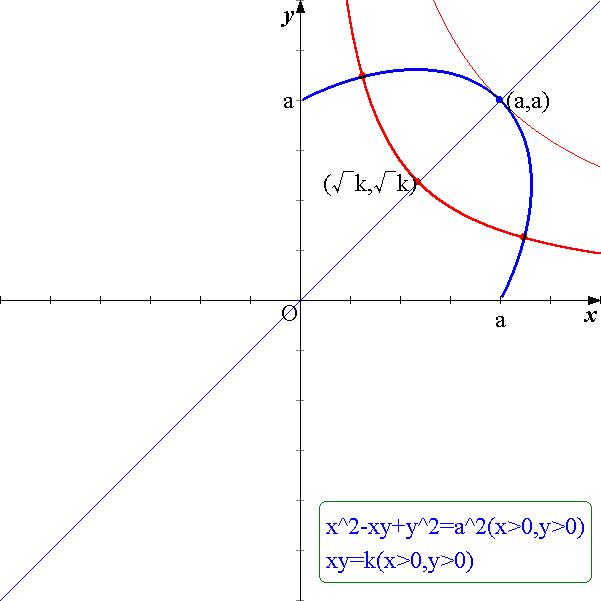
偙偙偱丆
仮俙俹俻亖侾乛俀丒俙俹丒俙俻丒sin佢俹俙俻亖併俁乛係丒倶倷
偮傑傝倶倷偺抣偺併俁乛係攞偑仮俙俹俻偺柺愊偱偁傞偺偱丆倶倷偺抣偺斖埻傪媮傔傟偽傛偄丏
倶倷亖倠乮亜侽乯偲偡傞偲丆偙傟偼倶幉丆倷幉傪慟嬤慄偲偡傞捈妏憃嬋慄偱偁傞丏
恾俀偐傜丆倶倷亖倠偑嵟戝偲側傞偺偼丆偙偺憃嬋慄偑揰(倎丆倎)傪捠傞乮愙偡傞乯偲偒偱偁傞偺偱丆
偙偺偲偒丆
丂丂倠亖倎2
偮傑傝丆倠偺抣偺斖埻偼丆
丂丂侽亙倠亝倎2
偱偁傞偺偱丆媮傔傞摎偼丆
丂丂侽亙仮俙俹俻亝併俁乛係丒倎2
偱偁傞丏

| NO.1072 | 2001.10.24. | 悈偺棳傟 | 嬌戝抣偲嬌彫抣偺嵎乮俁乯 |
10寧23擔偵乽昹揷乿偝傫偐傜掶惓偺偛巜揈傪庴偗庢傝傑偟偨丅師偺傛偆偵偟傑偡丅
乽倶偺俁師娭悢丂倖(倶)亖倎倶俁亄倐倶俀亄們倶亄倓丂乮倎亜侽乯
偑倶亖兛偱嬌戝抣傪偲傝丄倶亖兝偱嬌彫抣傪傕偮偲偒丄
嬌戝抣偲嬌彫抣偺嵎傪丆倎丄兛丄兝偱昞偣丅乿
栤戣侾丏摫娭悢倖亴(倶)亖侽偑堎側傞俀偮偺幚悢夝傪帩偪丄
偦偺夝偑兛丄兝偱偁傞偙偲傪棙梡偟偰夝偄偰偔偩偝偄丅
栤戣俀丏娭悢倖(倶)傪旝暘偡傞偲丄倖亴(倶)偱偡偑丄媡偵丄
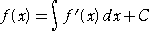
偱偁傞偙偲傪棙梡偟偰傕夝偗傑偡丅

| NO.1073 | 2001.10.24. | yokodon | 惓嶰妏宍偺撪晹傪摦偔慄暘乮係乯 |
No.1067 偺夝摎偱偡偑丄
梋尫掕棟偐傜 p , q 偺忦審幃傪弌偡偲偙傠傑偱偼椙偄偺偱偡偑丄栤戣偼偦偺屻偱偡丅
偙偙偱偼娙扨偺偨傔丄揰俹丄俻偑曈偺椉抂傕娷傔偰摦偔傕偺偲偟傑偟傚偆乮戣堄偲
偼堘偄傑偡偑乯丅
偙偺傕偲偱丄p, q 偼嫟偵 0 亝 p,q 亝 2 偺斖埻傪摦偒傑偡偑丄0 偲 2 偺偁偄偩
偺慡偰偺幚悢傪偲傟傞偐偳偆偐偼帺柧偱偼偁傝傑偣傫丅
幚嵺丄杮栤偺応崌丄併3 亙 a亙 2 偺壖掕偑偁傞偺偱丄
p , q 偼 0 亝 p,q 亝 2 偺斖埻傪楢懕偵摦偗傑偣傫丅
偙偺偙偲傪丄恾偱峫偊偰傒傑偟傚偆丅
峫偊摼傞忬嫷偼丄埲壓偺俁偮偱偡丅
乮i乯 0 亝 p,q 亝 1
乮ii乯 0 亝 p 亝 1 亙 q 亝 2 丄枖偼 0 亝 q 亝 1 亙 p 亝 2
乮iii乯 1 亙 p,q 亝 2
乮i乯偺応崌偼丄a 偺忦審偐傜晄壜擻偱偡丅
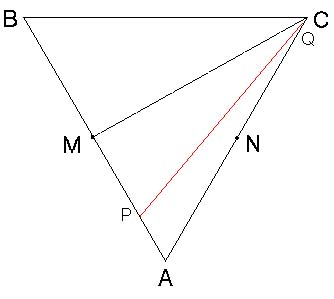
乮ii乯偺擇偮偺応崌偼丄曈俛俠偺拞慄偵娭偟偰懳徧堏摦偡傟偽杮幙揑偵摨偠忬嫷傪
昞偡偺偱丄慜幰偱峫偊傑偡丅
嶰妏宍俙俛俠偺曈俙俛丄曈俙俠偺拞揰傪偦傟偧傟俵丄俶偲偟傑偡丅偙偺偲偒丄揰俹
偼慄暘俙俵忋丄揰俻偼慄暘俶俠忋偵偁傝傑偡丅揰俹偑揰俙偲堦抳偡傞偲偒丄俠俻亖2
- a 偱偡偹丅偙偙偱丄揰俹傪揰俛偺曽岦偵摦偐偟偰傒傞偲丄揰俙偑揰俵偵帄傜側偄偆
偪偵丄揰俻偼揰俠偵摓拝偟偰偟傑偄丄偦偙偱慄暘俹俻偼偮偭偐偊偰偟傑偄傑偡丅
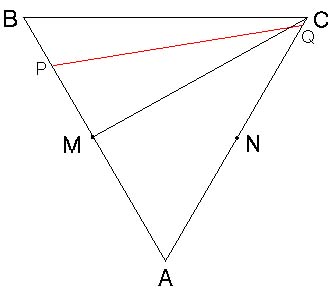
乮iii乯偺応崌偼丄乧僐儗偑嵟傕巚偄偮偒傗偡偄偲巚傢傟傑偡偑乧丄摉弶揰俹偑揰
俛偵堦抳偟偰偄偨偲偒丄揰俻偼慄暘俠俻忋偵偁傝傑偡偹丅偦偙偐傜揰俹傪揰俙偺曽岦
偵摦偐偡偲丄偁傞偲偙傠偱慄暘俹俻偼曈俛俠偵暯峴偵側傝傑偡丅偦偙偐傜峏偵摦偐偡
偲丄偁傞偲偙傠傑偱揰俹偑棃偨偲偒偵丄揰俻偼揰俠偵堦抳偟偰偟傑偄丄偦偙偱偮偭偐
偊偰偟傑偄傑偡丅
椺偊偽丄a 亖 11/6 摍偲偟偰丄幚嵺偵幚尡側偝偭偰傒傞偲丄忬嫷偑暘偐傝傗偡偄偲
巚偄傑偡丅

 E-mail
E-mail
 栠傞
栠傞