Weekend Mathematics/コロキウム室/NO.117
| NO.990 | 2001.7.15. | 水の流れ | 放物線の弧の長さ(1) |
太郎さんは、先日、卒業生が今大学で、こんな問題がだされています。
分からないので解いてくださいと 他の先生に頼んでいたのを聞きましたので、
今回の応募問題にしました。

曲線C:√x+√y=1について、
問題(1)曲線C、x軸およびy軸によって囲まれる部分の面積を求めよ。
問題(2)曲線C、x軸およびy軸によって囲まれる部分をx軸のまわりに
1回転させてできる回転体の体積を求めよ。
問題(3)曲線Cの長さを求めよ。<答 1+(√2/2)log(√2+1)>
<水の流れ:コメント>実はこの解法がくせ者でして、すらっとでてきません。
もし、聡明な皆さんで、解法を教えてくださればありがたいです。
問題(4)曲線C、x軸およびy軸によって囲まれる部分をx軸のまわりに
1回転させてできる回転体の表面積を求めよ。

| NO.991 | 2001.7.16. | yokodon | 正七角形(3) |
(その後思考を巡らして気付いたものですが)
最後の行の“=1/10”をどう導くか?ですが、過日お送りした分では計算機の
力を借りましたが、例えば以下のように導けるみたいです。
方程式 z7+1=0 の解の一つが、以下であることを利用します。
z = cos(π/7)+i sin(π/7)
方程式の左辺を因数分解し、この解を代入して(z+1)を落とし、実数部分をとる
と以下になります。
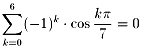
これに、cos(kπ/7)=-cos(π-kπ/7) k = 1〜6 …を利用して整理すると、最終
的に以下を得ます。
cos(3π/7)-cos(2π/7)+cos(π/7) = 1/2
結局、円分方程式の応用として、この関連でいろいろ議論できそうな感じですね( でも、高校の期末試験の問題としては、オリジナルのままでは、些か難しすぎそうで す;大学入試としても、標準〜ちょっと難しめ?かも知れません)。
余り意味のない一般化かも知れませんが、「水の流れ」さん御提起の問題は、以下 のように一般化することが出来そうです。
『正(2n+1)角形の一辺に平行な対角線 n-1 本(n≧3)について、その全ての線分長 の逆数の総和をとると、その値は件の正多角形の一辺の長さの逆数に等しい。』
きちんと確かめたわけではなくて、現段階では単なる予想ですが、ちょっと面白い
と思いました。(予想される)証明過程は、もし証明可能なら今回の n = 3 の場合
と本質的に同じ計算になりそうです。

| NO.992 | 2001.7.16. | yokodon | 放物線上の格子点 |
模試シリーズ1
xy 平面上の座標成分の値が整数であるような点を、格子点という。
(1)曲線C1:y = (√2)・x(x-1) 上の格子点を、全て求めよ。
(2)a、b、c を実数とする。
曲線C:y = ax2+bx+c 上に3個の相異なる格子点が存在するなら、この曲線C
上には無限個の格子点が存在することを証明せよ。
この問題から、放物線上の格子点の個数は、0,1,2,無限のいずれかであるこ
とが議論できます。
曲線上の格子点の問題は、つい先だって最終的な解決を見た『フェルマーの最終定
理』の証明での一つのキーポイントだったはずで、そこまで今回の問題から持ってい
くのはかなり長い道のりですが、そういうスレッドを作ってみるのも面白いのでは無
かろうか?…と、ちょっと思いました。

| NO.993 | 2001.7.17. | yokodon | 放物線の弧の長さ(2) |
No. 990 の問3の解答
問1と問2は比較的易しいと思われるので、問3だけきちんとした略解?を与えた
いと思います。問1の答の面積の値をS、問2の体積の値をVとすると、以下のよう
になりまして、比較的単純な積分計算で可能なはずです。
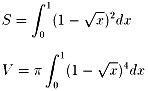
問4については、求める表面積をTとすると、以下のようになります。公式の導出
には、大学教養レベルの微分積分学の知識が必要ですが(導出を開陳して宜しければ
、後日お送りします;或いは、どなたかがお書きになるかも知れませんね)、一応公
式を提示したいと思います。
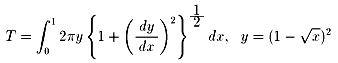
では、問3です。あんまり洗練された解法ではないかも知れませんが、素直な解法
を示したいと思います。求める長さをLとします。
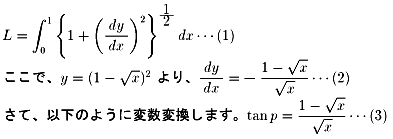 (訂正7/30)
(訂正7/30)
(1) に (2) を代入し (3) を用いて整理すると、以下のようになります。
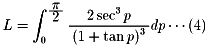
更に整理して、三角関数の加法定理を用いて変形し、
q=p+π/4 ・・・(5) (訂正7/30)
の様に変数変換をすると、以下のようになります。
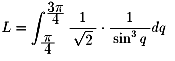
あとは、被積分関数の分母と分子に sin(q) をかけて、
sin2q=1-cos2q
の関係を用いて有理関数の積分に持ち込むことができます。
結局、以下の積分を実行することに帰着されます。
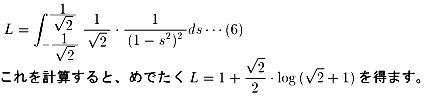
曲線を以下のようにパラメータ表示しても出来そうです
(が、ドツボにはまりそうです)。
x=cos4(u)、y=sin4(u) 0≦u≦π/2
この場合は、例えば、以下のようになります。
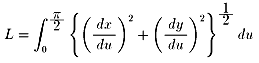
ところで、
(dx/du)2+(dy/du)2=2sin22u・(1+cos22u)
となるので、tan r=cos 2u 等と変数変換すれば、積分を実行することが出来るは
ずです。
ただ、最終的には [6] の積分を計算することに帰着するものと思われます。

| NO.994 | 2001.7.17. | DDT | 放物線の弧の長さ(3) |
問題(3)曲線Cの長さを求めよ。<答 1+(√2/2)log(√2+1)>
ベタな方法なのですが、とにかくやってみました。
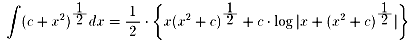
を使用します。
[手順1:ルートは嫌だ]
x1/2+y1/2=1とルートが二個も出てきてややこしいので、とにかくルートを消去します。
y1/2=−x1/2+1
y=(−x1/2+1)2
=x−2x1/2+1
2x1/2=x−y+1
4x=x2+y2+1−2xy−2y+2x
x2−2xy+y2−2x−2y=-1
(x−y)2−2(x+y)=-1 (1)
[手順2:式の形に合いそうな座標系を選んでみる]
二次形式論を使うのがすじのような気もしますが、単純に考えて、x−y=α,x+y=βとおくのが良さそうです。α-β系で式(1)は、
α2−2β=-1
β=1/2・(α2+1) (2)
[手順3:線素を計算する]
x−y=α,x+y=βより、x=(α+β)/2,y=(−α+β)/2なので、
dx=( dα+dβ)/2
dy=(−dα+dβ)/2
となり、
| dx2+dy2 | =(dα2+2・dαdβ+dβ2+dα2−2・dαdβ+dβ2)/4 |
| =(dα2+dβ2)/2 |
| (dx2+dy2)1/2 | =(dα2+α2・dα2)1/2/21/2 |
| =|dα|・(1+α2)1/2/21/2 |
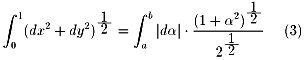
となります。
[手順4:α-β系での積分範囲,式(3)のa〜bを定める]
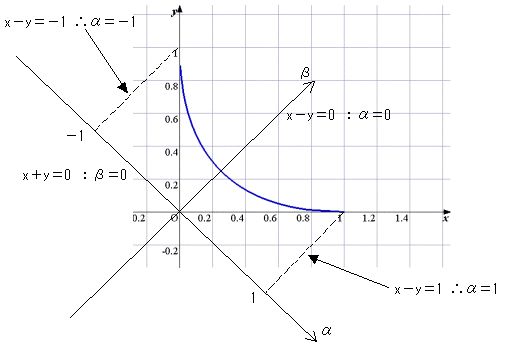
図より、α=−1〜1とすれば、dα>0で、|dα|=dα
[手順5:計算!]
式(3)より、
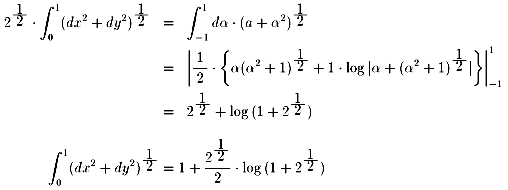

| NO.995 | 2001.7.23. | なか | 4444の問題(12) |
貴ページで4444の問題をおみかけして、
以前につくったプログラムを走らせてみました。
.4という表現はいんちきかもしれませんが、
参考までにお知らせします。
67=√4+(√4+4!)÷.4

 E-mail
E-mail
 戻る
戻る