Weekend Mathematics�^�R���L�E�����^NO.116
| NO.980 | 2001.7.1. | ���̗��� | �����p�`�i�P�j |

���Y����́A�Z���̎��̓e�X�g�����l���Ă��钆�ŁA����Ȗ������܂����B
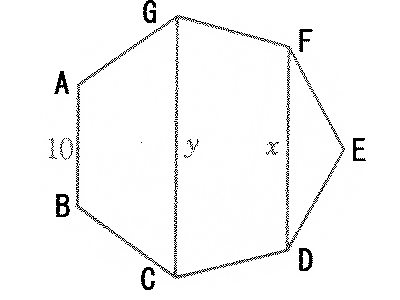
�@��ӂ̒������P�O�����̐����p�`�`�a�b�c�d�e�f������܂��B�}�̒��ɂ���Q�̑Ίp���c�e�Ƃb�f�̒������������A�������Ƃ���Ƃ��A
�P�^���{�P�^���̒l�����߂Ă��������B

| NO.981 | 2001.7.1. | �n���@�� | �����`�̐܂莆 |
�w�����Ɉꖇ�A�����`�̎�������܂��B�@
���̐����`�̖ʐς�1�Ƃ��āA���̂V���̂P�i�V�|�P�j�̑傫���ƂȂ鐳���`������ĉ������B�x
�w�����Ɉꖇ�A�����`�̎�������܂��B�@
���̐����`�̖ʐς�1�Ƃ��āA����30���̑傫���ƂȂ鐳���`������ĉ������B�x
�w�����Ɉꖇ�A�����`�̎�������܂��B�@
���̐����`�̖ʐς��P�Ƃ��āC���̂V���̂R�i�V�|�R�j�̑傫���ƂȂ鐳���`������ĉ������B�x
�w�����Ɉꖇ�A�����`�̎�������܂��B�@
���̐����`�̎����g���āA�O�̕ӂ̔䂪�@�T�F�P�Q�F�P�R�ƂȂ�O�p�`������Ă��������B�x
������,�@b�̒����`��������܂��B�@
�e��a�̒��_, b�̒��_�����Ԓ�����܂���Ƃ�
�āA���̒����`����܂����Ƃ��A�܂�ꂽ���̎��̒��_�̈ʒu�����߂�B
�w�����Ɉꖇ�@�����`�̎�������܂��B�@
���̐����`�̎����g���ĎO�̕ӂ̔䂪�X�V�F�U�T�F�V�Q�ƂȂ�O�p�`������Ă��������B�x

| NO.982 | 2001.7.9. | ���̌� | �Q�����̖��i�P�j |
�Q����
| ���F(x-1)/2=-z-2,y=-1 |
| ���F(x+1)/3=1-y=1-z |

| NO.983 | 2001.7.9. | ���̌� | ����̐ؒf |
�`,�s,�f,�b�̎l�̉������A�S���łT�Q�S�R����܂��B
���̂����f�Ƃb�͂��ꂼ��Q�O���A�`�Ƃs�͂��ꂼ��R�O������܂��B
�`,�s,�f,�b�͊�ɕ���ł��܂��B
�y�f�`�́i�`�f���b�s�j
�y�f�a�́i�s�s�s���`�`�`�j
�y�f�b�́i�f���f�`�s�b�b�j
�y�f�c�́i�f�b���f�f�b�b�f�b�j
�Ƃ����z��́��̕�����ؒf���܂��B
�e�y�f�`,�a,�b,�c�͉������ؒf����ƍl�����܂���

| NO.984 | 2001.7.10. | yokodon | �����p�`�i�Q�j |
�O�ډ~�̔��a�� r �Ƃ���ƁA
�@10��2r�~sin(��/7)�@�E�E�E[1]
�@������ x�Ay �ł�������̗��[�ł��钸�_�����ꂼ��`�A�a�y�тb�A�c�Ƃ��A�O��
�~�̒��S���n�Ƃ��A�O�p�`�n�`�a�y�юO�p�`�n�b�c�ɂ��Đ����藝��K�p����ƁA
�@sin(��/14)/r�� sin(6��/7)/y�@�E�E�E[2]
�@sin(3��/14)/r��sin(4��/7)/x�@�E�E�E[3]
�@������p���āA1/x�{1/y ���v�Z���܂��B
| 1/x�{1/y | ��(1/r){sin(��/14)/sin(6��/7)+sin(3��/14)/sin(4��/7)} |
| ��(sin(��/7)/5){sin(��/14)/sin(��/7)+sin(3��/14)/sin(3��/7)} | |
| ��(1/5)�~{sin(��/14)+sin(��/7)/(2cos(3��/14))} | |
| ��(1/5)�~{sin(��/14)+sin(6��/7)/(2cos(3��/14))} | |
| ��(1/5)�~{sin(��/14)+2sin(3��/14)cos(3��/7)} | |
| ��(1/5)�~{sin(��/14)+sin(9��/14)-sin(3��/14))} | |
| ��(1/5)�~{cos(3��/7)+cos(��/7)-cos(2��/7)} | |
| ��1/10 |

| NO.985 | 2001.7.10. | ���� | 2001���{���w�R���N�[�� |
�Q�P���I�̐V�����Ȋw�E�Z�p�̊�Ղ�S�����ƃ��}�����߂���҂̍˔\�@���A
�琬���Ă������߂�1990�N�x����A���{���w�R���N�[�����A
1997�N�x������{�W���j�A���w�R���N�[�����J�Â��Ă��܂��B
�P�D���R�ɂ������ƍl����
���Ԃ͖�5���ԁA�r���Œ��H����ݕ��Ȃǂ͎��R�Ɏ�邱�Ƃ��ł��܂��B
�܂��A�Q�l����m�[�g�A�d��Ȃǂ̎������݂����R�ł��B
�Q�D�V�������w�̔���
�w�Z�ɂ����鋳��ے��A���ȏ��ɂƂ��ꂸ�A���w�I�Ȗ{���ɍ��������A
�l���Ċy��������܂��B
�R�D���ʂȍ˔\�̔���
�D�G�ȍ˔\�����������k�A���j�[�N�Ȕ��z�����������k�ȂǁA�l�X�ȎQ���҂̍˔\
�𑽖ʓI�ɕ]�����邽�߂ɁA����������������k�����łȂ��A
�P��ɏW�����đf���炵�����z���o�������k�ɂ��܂�^���܂��B
�@
�S�D�l�ނ̈琬
�R���N�[���Q���҂̐��w�I�\�͂�����ɍ��߂邽�߁A�R���N�[���̕\�����̌�A�u�]����s���܂��B
��l�ł������́A���w�ɋ����̂��鍂�Z���̊F����̎Q�������҂��܂��B���{���w�R���N�[���ψ���
�u��1�Q����{���w�R���N�[����W�v���v
�P�D�J�Ó����F�@�@�����P�R�N�W���P�W���i�y�j�P�O���t���@���Ԃ͂P�O���R�O������P�U���܂�
�Q�D��@��@�F���É���w����w���i�ڍׂ͎Q���ɂĒj
�R�D�Q�����i�F���Z���A���Z�������N��̎�
�S�D������@�F���̗v�̂ɏ]���ĉ����t���ŕ����P�Q�N�V���P�X���i�j���K�����܂łɐ\�����ނ���
�T�D�Q�����@�F�Q�O�O�O�~�@�������ɂďW�߂܂��B
�U�D���̑��@�F
�i�P�j���H�͊e���Ŏ��Q���邱�ƁB���H���Ԃ́A�e�������R�ɐݒ肵�A ���̎����ɂ������Ă悢�B�������A��ꂩ��O�ւł邱�Ƃ͂ł��Ȃ��B�Љ�̋����͒����Ă��܂��B��_�썂�Z�@���w�ȁ@����
�i�Q�j�Q�l���A�m�[�g�A�d�쓙�̎������݂͎��R�Ƃ���B�������A���Ɋւ��鎄��͋֎~����
�i�R�j�����t���͎��̇@�`�H������Ȃ��L�����邱�ƁB���M�A�ԐM�̈ʒu���ԈႦ�Ȃ����ƁB �܂��A�\�����݂́A�P�ʂɂ���l�݂̂Ƃ���B
�@�@�X�֔ԍ��A�Z���@�A�@�d�b�ԍ��@�B�@�w�Z���i�t���K�i�j�@�C�@�w�N�@ �D�@�w�Z���ݒn�i�s���{���y�юs�����܂Łj�E�@�����i�t���K�i�j�@�F�@���ʁ@�@ �G�@���N�����@�H�@�ی�Ҏ����i�ی�Ғ��M�@�A���j
�i�S�j�R���N�[���Ɋւ���₢���킹�́A���É���w�����ۓ��A���{���w�R���N�[���W
�@�@�@�d�b�@�O�T�Q�|�V�W�X�|�Q�O�P�P
�@�@�@���ԁ@�X�F�O�O�`�P�Q�F�O�O�ƂP�R�F�O�O�`�P�V�F�O�O�i�y�A���͏����j

| NO.986 | 2001.7.10. | ���� | 2001���{���w�R���N�[���_���� |
�Q�P���I�̓W�]���J����҂̍˔\�@���A�琬���Ă������߂ɁA
1990�N�x������{���w�R���N�[�����A1997�N�x����͕����ē��{�W���j�A���w�R���N�[����
�J�Â��Ă��܂��B
�@���̂��сA2000�N����V���ȓ��{���w�R���N�[���_���܂��n�݂���܂����B
�P�D���R�ɂ������l����
�_���̓e�[�}�̔��\������ߐ�܂Ŗ�R�P���A�������Ǝ��R�ɍl���A
����ɁA�}���ق�C���^�[�l�b�g�Ȃǂ𗘗p���Ē��ׁA��������_�������҂��܂��B
�Q�D�V�������w�̔���
�w�Z����A���ȏ��ɂƂ��ꂸ�A���w�I�̖{���ɍ��������A�l���Ċy�����e�[�}����܂��B
�R�D���ʂȍ˔\�̕]��
�Ȗ��Ș_�ؗ́A���m�Ȍv�Z�͂����łȂ��A�Ǝ����̂��邷�炵�����z��
����N�������]�����܂��B
�S�D�l�ނ̈琬
���I�_���̂������ɗD�G�Ȃ��̂́A���w�R���N�[���t�H���[�A�b�v�Z�~�i�[�ł��鐔���E�F�[�u
�ŏЉ��܂��B�@
��l�ł������́A���w�ɋ����̂��鍂�Z���̊F����̎Q�������҂��܂��B
�@�@���{���w�R���N�[���ψ���
�u��Q����{���w�R���N�[���_���ܕ�W�v���v
�P�D���厑�i�F
�@���{���w�R���N�[���_���܁@���Z���ȏ�i��ʂ̕����j�B
�����_�������}���܂��B
�A���{�W���j�A���w�R���N�[���_���܁@���w���ȉ��B�����_�������}���܂��B
�������A�����_���̏ꍇ�����w���ȉ��ł��邱�Ƃ�v���܂�
�Q�D�_���e�[�}�F�@���̘_���e�[�}����A�ЂƂ�I��ŁA�_���ɓZ�߂ĉ������B
�@�y�p�b�`���[�N�z�싅�̃{�[�����悭�݂�ƁA�����`�̓̔炪�O�O�ɂʂ����킳��Ă��邱�Ƃ��킩��܂�
��ɉ���钣�͂��Ȃ�ׂ��ϓ��ɂȂ�悤�ɁA��̌`������g�Ȑ��ɂȂ��Ă���悤�ł��B����ȍH�v�͂ǂ����琶�܂ꂽ�̂ł��傤���B�܂��A���̔�̌`���{�[�����������̂ɓK���Ă��邱�Ƃ��A�ǂ̂悤�ɐ����ł��邩�B
�@���̖��ɓ�����悤�Ȑ��𗧂ĂĂ݂Ă��������B�����ē��l�̍l����K�p���āA
�h�[�i�c�^�̋Ȗʂ�̃S���̔������ʂ����킹�Ă��������܂����@���Ă��Ă݂Ă��������B
�A�y�R�����̉����Ɣ���z�����`���A��������Z�����̕ӂ���ӂƂ��鐳���`��藎�Ƃ��Ăł��钷���`�Ɠ����`�i�����j�ɂȂ�Ƃ��A���̒����ӂƒZ���ӂ̒����̔��������Ƃ����܂��B������̓o�����X�̂Ƃꂽ�������`�ɗǂ��\����鐔�Ƃ��ėL���ł��B���Ƃ��A���܊p�`�̑Ίp���ƈ�ӂ̒����̔�͉�����ɂȂ��Ă��܂��B
�@�܂��A�����`�������ɐ܂肽�������`�Ƒ����ɂȂ�Ƃ��A�����ӂƒZ���ӂ̒����̔�𔒋��Ƃ����܂��B���{�Ŏg���Ă���m�[�g�͂��̌`�����Ă��āA�����͎��p�I�ł���Ƃ��������ł��ˁB
�@�����Ƃ̂`���͓W����ɏo�����߂ɁA�R�����̉�����Ɣ����Ƃ����C���[�W�ō\�z������Ă��܂����A���Ȃ�����̒����̂�������Ɣ����̃C���[�W�ɂ����悤�ɂ��悤�Ƃ�����A���ꂼ��̒����̂̕ӂ̒����̔���ǂ̂悤�ɂ��܂����B
�@�܂��A�ق��̗��̂ł͂ǂ��ł��傤���B�@
�R�D������@�@�F�_���͂`�S�ʼn��������e�p���i�Q�O�~�Q�O�j��p���邱�ƁB
�����͕��͂ƕ����A�s�����߂ď������ƁB�K�v�ɉ����Đ}�����Ă��\��Ȃ��B
�����̐����͂Ƃ��ɂȂ��B
���@�_�����t��@�X�֔ԍ��S�U�S�|�W�U�O�P�@���É��s����s�V��
�@�@�@�@�@�@�@�@���É���w�����ۓ��A���{���w�R���N�[���S��
�@�@�@�@�@�@�@�@���@�����Ɂu�_���܁v�Ǝ鏑���̂���
�S�D���ߐ�F�����P�R�N�W���P�W���i�y�j�K��
�Ȃ��A�����͓��{���w�R���N�[���A���{�W���j�A���w�R���N�[�������É���w�ŊJ�Â���܂��̂ŁA
�_�������Œ�o���Ă����܂��܂���B
�T�D�R�����@�F���{���w�R���N�[���_���܁A���{�W���j�A���w�R���N�[���_���܂Ƃ��ɁA
����_�����ꂼ��ɁA�Q���̍��ǎ҂����nj��ʂ����|�[�g�ɂ܂Ƃ߁A
�R�����̍��c�ɂ����I�_�������肵�܂��B
���@�R����@�ɓ��@���V�i���É���w�����A���{���w�R���N�[���ψ����j
�@�@�@�@�@�@�@���@���v�i���É���w�����A���{���w�R���N�[���ψ�����ψ���ψ����j
�@�@�@�@�@�@���̑����{���w�R���N�[���ψ�����ψ���ψ����
�U�D�\�����F�\���͐��w�R���N�[���\���������ɍs���A�ŗD�G�_���ɑ��Ă͓��{
���w�R���N�[���_���܁A���{���w�W���j�A���w�R���N�[���_���܂Ƃ����w�R���N�[�����
�Ɠ����̋L�O�i����яܕi�悵�܂��B
�D�G�_���ɑ���\�������w�R���N�[���ɏ����܂��B
�܂��A�ŗD�G�_���̌��ʂɂ��ẮA�����V���ɏЉ�܂��B
�V�D�_���Ɋւ���₢���킹�́A���É���w�����ۓ��A���{���w�R���N�[���S��
�@�@�@�@�@�@�@�d�b�@�O�T�Q�|�V�W�X�|�Q�O�P�P
�@�@�@�@�@�@�@���ԁ@�X�F�O�O�`�P�Q�F�O�O�ƂP�R�F�O�O�`�P�V�F�O�O�i�y�A���͏����j
���\������11���R���i�y�j�j���ɖ��É���w�V���|�W�I���ōs���܂��B
�Љ�̂v������ł̌f�ڂ̋����͓��Ă���܂��B��_�썂�Z�@���w�ȁ@����

| NO.987 | 2001.7.11. | �c�c�s | �����i�Q�j |
���� ���̂Q�i�܂���ߎ� �� ðװ�����j
�Ȃ���������̂��H�Ǝv�������Ƃ�����܂��B���_�Ƃ��āA�������Ƃ����z���Ƃ���
���̂܂ܑ����قǐl�Ԃ͊�p����Ȃ����炾�A�Ǝv���܂����B
����������ɂ����`�����s���āA�P�����ƑΔ䂵�ĂȂ�Ƃ������Ă���̂��ƁB
�Ȃ��P�����ȂH�Ǝv�������Ƃ�����܂��B�P�����́A
�|���Z�Ƒ����Z�Ōv�Z�ł��邩�炶��Ȃ��̂��A�Ǝv���܂����B
�����Ŏl�����Z�́i�|���Z�́j�A���@�i�����Z�j���瓱���܂��B
�Ȃ������Z�ȂH�Ǝv�������Ƃ�����܂��B�l�Ԃ͊�{�I�ɔn��������A
���ϓI�ɗ����ł���̂͑����Z��������Ȃ��ł��傤���H�@�l�Ԃ̔\�͂̈ꕔ��
���f���������Ǝv������߭������A��{�I�ɑ����Z�����ł��Ȃ��̂́A���̂����Ȃ̂��ƁB
�����炱�������ɂ����`���Ȃ̂��ƁB
�Ƃ���Łm����1�n���A����1�_��1�_��1�������Z��ł���ƍl���Ă��A����������
�Ȃ��̂ł���A���̂P�_�̋ߖT���������Ŕ`�����Ƃ��ɂ́A
���}�̂悤�ȑ��������Ă��ǂ��͂��ł��B
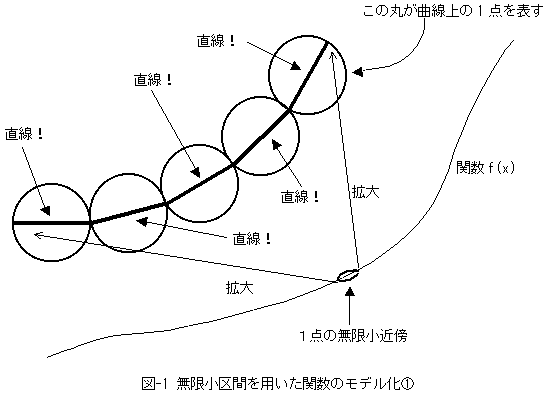
�������A�}-1�̂悤�Ȃ��̂��{���Ɍ�����킯�͂Ȃ��̂ŁA�}-1�͊��̃��f�����@�ƌĂ��
�����܂��B�����������ɍl���Ă�������`�`�A���炢�̈Ӗ��ł��B�������Ȃ���
�}-1�́A�����A����1�_�̒��ɏZ�ޒ�������\�����ꂽ�܂���̏W�܂�Ƃ݂Ȃ��A�Ƃ����Ӗ��ł��B
�����Ē����͊|���Z�Ƒ����Z����v�Z�ł��܂��B��������ƁA�����̌p�������ł���C�ӂ̊��́A
�|���Z�Ƒ����Z�����Ōv�Z�ł���̂ł͂Ȃ����H�Ǝv���Ă��܂��B
���ꂪ�e�[���[�����ł͂Ȃ��̂��H�B���̍l���ɂ͋��͂ȏ����l�����܂����B
���Ƃ̊��ɑ���A�������Ƃ��Ẵe�[���[�W�J�̈�Ӑ��ł��B
�������͈͂Ő��藧�͂��̃��f�����@�͎��ۂɂ͕s�\�Ȃ̂ŁA
�����L���̑傫���ő傫���ŋߎ����Ă݂܂��B�Ⴆ�E�E�E
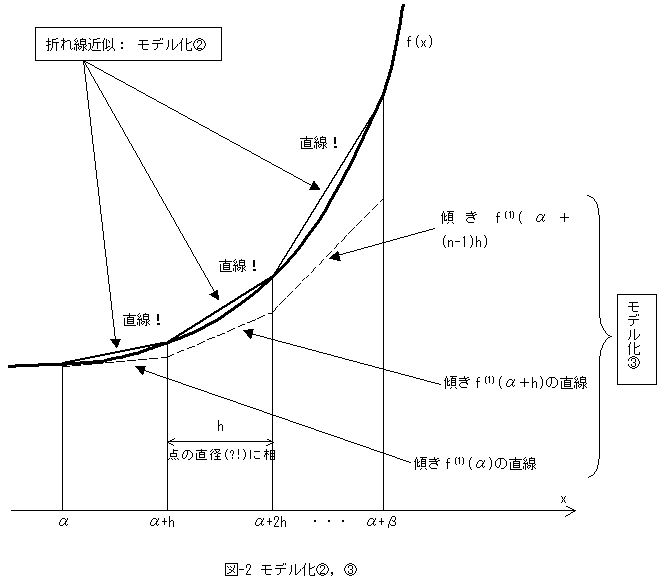
�}-2�̋�ԁm���C���{���n��n�������āA�e������ԂŋȐ�f(x)��܂���ߎ����܂��B�@
������Ԃ̕�h�́A���f�����@�ɂ�����Ȑ����1�_��\���~�̒��a�ɑ������܂��Bnh�����ł��B
��������f�����A�Ƃ��Ă����܂��B�������łȂ��傫���������f�����A�́A
�������̃��f�����@�ɑ���A�L���̑傫���ł̋ߎ����f���ł��B
�������f�����@�ƇA���A�{���ɑΉ�����̂ł���A������ԕ�h��h��0�̋Ɍ��ŁA
�@�ƇA�͈�v����͂��ł��B�����Ƃ����Ah��0�̋Ɍ��ŁA�A�߂Â����f����������Ƃ���A
�����h��0�̋Ɍ��Ŗ{���̃��f�����ł���@�Ɏ�������͂��ł��B
�����ł͐}-2�̃��f�����B���g���܂��B���f�����B�́A�e������Ԃ̉��[�̌X�����������ŁA
���f�����A������ɋߎ��������̂ł��Bf(j)(x)�́A��f��j�K������\�����̂Ƃ��܂��B
�Ƃ��낪���f�����B�ɂ́A�B������ɋߎ��������f�����C�������Ɏv�����܂��B
�ʓ|�����ă��f�����C��}�ɂ͂��܂���ł������A
�����̈Ӗ�����`�����삻�̂��̂Ƒ����邱�Ƃ���A���ڏo�Ă��܂��B
�m���f�����C�n
����nh�Ȃ̂ŁA
�@�@f(���{��)��f(���{nh)�ł��B
�@�@f(���{nh)�`f(���{(n�|1)h)�{h�f(1)(���{(n�|1)h)
�Ƃł��܂��B�����n�̕�����Ԃ̍Ō��n�ڂ̋�Ԃɂ����āA���̉��[�̊��l�ƌX���ŁA
h�i��[�̊��l��\�����ł��Bn��1�̏ꍇ���l����A�ӂ��̔����̌`�ł����A
���f�����B���̂܂܂ł��B�������Ƃ�(n�|1)�ڂ̋�Ԃł��ł���͂��ł��B
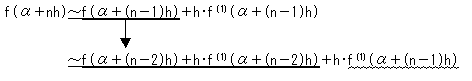
�����̂Ƃ��낪���̕����ł��B�����̉E�ӑS�̂��݂�A���f�����B�����ŕ\�������̂ɂ����Ȃ�
���Ƃ��킩��܂��B�Ƃ���Ŕg�����ɂ��������Ƃ��ł���͂��ł��B�����ŁA�����̌`�A
f(���{h)�`f(��)�{h�f(1)(��)
���P�����ƍl���܂��B�v����Ɋ�f�ɐ����͂Ȃ��̂�����A
f(j)(���{h)�`f(��)�{h�f(j+1)(��)
�����Đ��藧���ėǂ��͂��ł����Ah�ɂ����ɐ����͂���܂���B���Ƃ���ƁA
f(1)(���{(n�|1)h)�`f(1)(���{(n�|2)h)�{h�f(2)(���{(n�|2)h)
�Ȃ̂ŁA
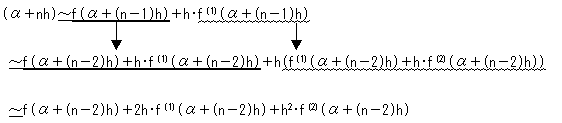
�ƂȂ�܂��B������Ԃ����X��m��k���āA(n�|m)h��0�ɂȂ�܂ŁA������J��Ԃ��܂��B
���������邽�߂ɁA��������n��1,2,3�̂Ƃ��Ɏ��s����ƁA
f(���{ h)�`f(��)�{ h�f(1)(��)
f(���{2h)�`f(��)�{2h�f(1)(��)�{h2�f(2)(��)
f(���{3h)�`f(��)�{3h�f(1)(��)�{3h2�f(2)(��)�{h3�f(3)(��)
�ƂȂ�A
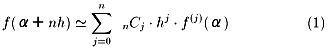
���\�z�ł��A���ۂɋA�[�@�ŏؖ����邱�Ƃ��ł��܂��B
��(1)�́A��ލ����̌����Ƃ��Ēm���Ă��܂��B
h��0�̋Ɍ��ł́A���f���C���B���A���@�Ǝ�������͂��ł��B�Ȃ��Ȃ炱���́A
�Ӗ��Ƃ��Ă݂͂ȓ����ŁA���̓���_�̓������ߎ��x��ς��ĕ\���Ă��邾���ł��B
��������ƃ��f���C����o�Ă�����(1)��h��0�ł̋Ɍ��́A�|���Z�Ƒ����Z������p�����C��
�̊��̕\���@�Ƃ������ƂɂȂ�܂��B���s����ƁA
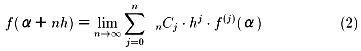
�ƂȂ�܂��B�ڋ��ɂ������ŁA�v�Z�̕��j���߂��s���܂��B
�܂�u����́A�e�[���[�����̐����ł����āA�ؖ��ł͂Ȃ��I�v�B
�����lim�ƃ��̋Ɍ����������Ȃǂ͈ՁX�ƍs���Ă��܂��A�����o�Ă���̂����A
�Ƃɂ������Ă݂܂��Bnh�����Ȃ̂�h����/n�ł��������A��(2)�̒��̈ꍀ�����o���āA
���̋Ɍ����ɂƂ�܂��Bn������Y�ꂸ�ɂ����Ȃ���A

�ƕό`���܂��Bj�͂����܂ŗL���ł��邱�Ƃɒ��ӂ��āAn�������v���o���ƁA
1�ɋ߂Â�()���L����j�Ȃ̂Ō��ʂ�1
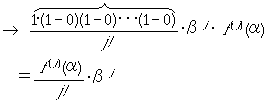
�������܂��B�Ɍ��������������ꂽ��(2)�ɖ߂��Ă����̍��v���Ƃ�A
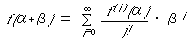
�ƂȂ�A�e�[���[�����ƂȂ�܂��B���������킯�Ńe�[���[�����́A
�܂���ߎ��̋Ɍ��̃X�g���[�g�ȕ\���Ƃ������ƂɂȂ�܂��B
���ꂪ��@�Ɖ��@�����Ő�������̂́A���ꂱ�����܂���ߎ�������ŁA
����1�_�ɂ͒������Z��ł���A�Ƃ������Ƃ̌��������ɂ����Ȃ��Ǝv���܂��B
�����ĔC�ӂ̊��̌v�Z�@�����@�����ŗ����ł���̂́A�ƂĂ��d�v�Ȃ��Ƃ��Ƃ��v���܂��B
���@���瓱����l�����Z�����l�Ԃ͗����ł��Ȃ��̂ł́H�Ƃ����Ӗ��ł��B
���Ƃ��ǂ�Ȃɓ���v�Z������Ă����Ƃ��Ă��A���̌v�Z�ߒ��ōŌ�ɂ��ǂ蒅���̂́A
�u�����Z���v�\�Ɓu�|���Z���v�\���Ǝv���邩��ł��B
���́A�P�s�ōςރe�[���[�̒藝�̏ؖ�������Ă݂悤�Ǝv���܂��B

| NO.988 | 2001.7.12. | Junko | �Q�����̖��i�Q�j |
�Q������}��ϐ��\�����܂��B
�������F(x-1)/2=-z-2 =S,y=-1�@���A
x=2s+1,y=-1,z=-s-2
�������F(x+1)/3=1-y=1-z�@=t ���A
x=3t-1,y=1-t,z=1-t
�܂�A��������̓_�o�́A�}��ϐ�s���g���āA�o(2s+1,-1,-s-2)�ƕ\����킯�ł��B
���l�ɒ�������̓_�p�́A�}��ϐ�t���g���āA�p(3t-1,1-t,1-t)�ƕ\���܂��B
��������̓_�o�ƒ�������̓_�p�Ƃ̋����̂Q��͈ȉ��̂悤�ɂȂ�܂��B
| �o�p�Q | ={(3t-1)-(2s+1)}�Q+{(1-t)-(-1)}�Q+{(1-t)-(-s-2)}�Q |
| =11t�Q+5s�Q-14ts+14s-22t+17 | |
| =5{s+7/5�(1-t)}�Q+6/5�(t-1)�Q+6 |
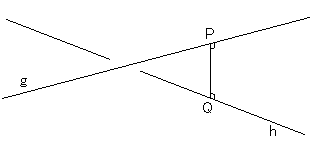
���̓_�o0�A�_�p0��ʂ钼�����A���҂ɐ����Ɍ���钼���Ƃ������ƂɂȂ�B
�]���ċ��߂钼���́Ax-2=y=z/2(���P)
��������̓_�o(2s+1,-1,-s-2)�ƒ�������̓_�p(3t-1,1-t,1-t)�̒��_���q�Ƃ���ƁA
�q( (2s+3t)/2,-t/2,(-s-t-1)/2 )�Ƃ�����B
x=(2s+3t)/2 �@(1) y=-t/2 �@(2) z=(-s-t-1)/2 �@(3)
������A�}��ϐ�����������ƁAx+y+2z+1=0
�܂肱��́A�o0�p0�̒��_��ʂ�A
�x�N�g���o0�p0��@���x�N�g���Ɏ��A���ʂł���B(���R)

| NO.989 | 2001.7.15. | M.Nakajima | �S�S�S�S�̖��(11) |
�K�E�X�L�����g���ĉ����Ă���l�����܂������A������g����
a�ȏ�a+1����(a�͐���)�̎��������ׂ�a�ɂȂ�̂ł�����ƃY���C��
�v���܂��i���̕����������̍l���Ă����̂Ə����Ⴄ�j�B
����Ȏ������Ȃ��Ă� tan(pi/4)�ipi = �~�����j���g���Ή����܂�
�iC(combination)���g���ƍX�Ɋy�ɉ�����j�B
67�ȊO�̐��̓K�E�X�L����
C(combination)���g�킸�ɕ\�����i�����Q�Ɓj�̂ł��� 67���K�E�X�L����
C���g�킸�ɕ\�����l�͋����Ă��������B
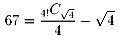

 E-mail
E-mail
 �߂�
�߂�