
Weekend Mathematics/コロキウム室/NO.113
| NO.953 | 2001.5.1. | 水の流れ | 最大数の確保(3) |
F(n,k)を三角形状に書いてみると、
|
(n k) |
0 |
1 |
2 |
3 |
4 |
5 |
・・・ |
計 |
|
1 |
1 |
1 |
||||||
|
2 |
1 |
1 |
2 |
|||||
|
3 |
2 |
3 |
1 |
6 |
||||
|
4 |
6 |
11 |
6 |
1 |
24 |
|||
|
5 |
24 |
50 |
35 |
10 |
1 |
120 |
||
|
6 |
120 |
274 |
225 |
85 |
15 |
1 |
720 |
|
|
・・・ |
皆さん!この配列された数列をよく見ると、何かを思い出します。
それは、多項式:x(x+1)(x+2)(x+3)(x+4)・・・(x+n-1)を展開したときの係数です。
さらに、この係数は、第1種スターリング数にもなっています。
また、次のような性質を持っています。
F(n,1)=(n-1)!
F(n,n-1)=1
F(n,0)+F(n,1)+・・・+F(n,n-1)=n!
問題5については、
(Ⅰ)最後の札がnであるとき:このときは、最後に必ず入れ換えをすることになるから、
k回の入れ換えが起きるための条件は、最後のnの札を除くn-1枚について、
k-1回の入れ換えが起きることになる。
(Ⅱ)最後の札がnでないとき:このときは、最後の札で入れ換えは起きないから、
k回の入れ換えが起きるための条件は、
最後の札を除くn-1枚について、k回の入れ換えが起きることである。
よって、 F(n,k)=F(n-1,k-1)+(n-1)×F(n-1,k)
実は、この漸化式が、第1種スターリング数の漸化式にもなっています。
問題6:期待値の関係は、漸化式を用いて、E(n)=E(n―1)+1/nがでてきます。
後は、E(n)=1/2+1/3+1/4+・・・+1/n になることは容易です。
出題の意図は、第1種スターリング数に魅力を感じたからです。

| NO.954 | 2001.5.1. | 水の流れ | 当たりくじ(1) |
太郎さんは、ときどき大学入試問題を見ています。
過去の東海大学の入試問題を参考にして出題します。
第1の箱、第2の箱、第3の箱、・・・、第nの箱と全部でn個の箱があります。
どの箱にもn本のくじが入っていて、当たりくじの本数は第k個の箱にはk本ある。
(k=1,2,3,・・・,n)
さて、(1)今、これらn個の箱から無作為に1個の箱を選び、
その箱からくじを無作為に1本取り出して、
くじを元の箱のもどしてまた同じ箱でさらに1本くじを引いたとき、
問題1:少なくとも1本当たりくじを引く確率を求めよ。
問題2:箱が無限に多くあったとき、少なくとも1本当たりくじを引く確率の極限値を求めよ。
また、(2)これらn個の箱から無作為に2個の箱を選び、
それらの箱から1本ずつくじを引きとき、
問題3:少なくとも1本当たりくじを引く確率を求めよ。
問題4:箱が無限に多くあったとき、少なくとも1本当たりくじを引く確率の極限値を求めよ。

| NO.955 | 2001.5.1. | 水の流れ | 和集合の要素の個数(3) |
包含と排除の原理
集合Sの中の部分集合をS(ai)と書き、その要素の個数をN(ai)とする。
また、集合S(ai)の補集合をS(ai)と書き、その要素の個数をN(ai)とする。
さらに、集合S(ai)と集合S(ak)との共通部分をS(aiak)と書き、
その要素の個数をN(aiak)とする。
ただし、i,k=1,2,3,・・・,nで、i≠kとする。
ここで、n=1のとき、全体集合Sの要素の個数N(S)をNとすると、
N=N(a1)+N(a1)より、N(a1)=N-N(a1)・・・①
n=2のときは、
N=N(a1a2)+N(a1a2)+N(a1a2)+N(a1a2)
したがって、
| N(a1a2) | =N-N(a1a2)-N(a1a2)-N(a1a2) |
| =N-{N(a1a2)+N(a1a2)}-{N(a1a2)+N(a1a2)}+N(a1a2) | |
| =N-N(a1)-N(a2)+N(a1a2)・・・② |
さて、n=3のときは、
| N= | N(a1a2a3)+N(a1a2a3)+N(a1a2a3)+N(a1a2a3) |
| +N(a1a2a3)+N(a1a2a3)+N(a1a2a3)+N(a1a2a3) |
この関係式を整理すれば良いのだが、3個の場合は容易ではない。
n=2のときの包除の原理の関係式②を利用して、導くことにする。
②の式で、全体集合Sの代わりにすでに、集合S(a3)について同じような関係式を作る。
N(a1a2a3)=N(a3)-N(a1a3)-N(a2a3)+N(a1a2a3)
したがって、
| N(a1a2a3) | =N(a1a2)-N(a1a2a3) |
| ={N-N(a1)-N(a2)+N(a1a2)} -{N(a3)-N(a1a3)-N(a2a3)+N(a1a2a3)} | |
| =N-N(a1)-N(a2)-N(a3) +N(a1a2)+N(a1a3)+N(a2a3)-N(a1a2a3)・・・③ |
次に、n個の集合の場合にも一般化した関係式を考えることができる。
その証明方法は、上に②から③を導いた同じ変形で、数学的帰納法できる。
では、一般の包除の原理は、
| N(a1a2・・・an) | = | N-N(a1)-N(a2)-・・・-N(an) |
| +N(a1a2)+N(a1a3)+・・・+N(an-1an) | ||
| ・・・・・・+(-1)nN(a1a2・・・an) | ||
| = | 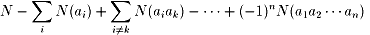 |
<証明>
自然数nに関して、数学的帰納法で証明します。
n=1のときは、①より証明済み
n=kのとき、上の関係式が成り立つと仮定する。
すると、全体集合Sの中で、k個の部分集合に関して、次の関係式が成立する。
| N(a1a2・・・ak) | = | N-N(a1)-N(a2)-・・・-N(ak) |
| +N(a1a2)+N(a1a3)+・・・+N(ak-1ak) | ||
| ・・・・・・+(-1)kN(a1a2・・・ak)・・・④ |
ここで、部分集合S(ak+1)に対する同じ関係式を作ると
| N(a1a2・・・akak+1) | = | N(ak+1)-N(a1ak+1)-N(a2ak+1) -・・・-N(akak+1) |
| +N(a1a2ak+1)+N(a1a3ak+1)+・・・+N(ak-1akak+1) | ||
| ・・・・・・+(-1)kN(a1a2・・・akak+1)・・・⑤ |
そして、N(a1a2・・・akak+1)を④-⑤から作ると、
| N(a1a2・・・akak+1) | = | N(a1a2・・・ak) -N(a1a2・・・akak+1) |
| = | N-N(a1)-N(a2)-・・・-N(ak) | |
| +N(a1a2)+N(a1a3)+・・・+N(ak-1ak) | ||
| ・・・・・・+(-1)kN(a1a2・・・ak) | ||
| -{N(ak+1)-N(a1ak+1)-N(a2ak+1)-・・・-N(akak+1) | ||
| +N(a1a2ak+1)+N(a1a3ak+1)+・・・+N(ak-1akak+1) | ||
| ・・・・・・+(-1)kN(a1a2・・・akak+1)} | ||
| = | N-N(a1)-N(a2)-・・・-N(ak+1) | |
| +N(a1a2)+N(a1a3)+・・・+N(akak+1) | ||
| ・・・+(-1)k+1N(a1a2・・・akak+1)
|
すなわち、n=k+1の場合にも成立しているを示しているので、数学的帰納法よりすべての自然数nについて、この定理は成り立つ。
この式は見た目より記憶しやすくなっていますから、覚え易いです。
【参考】
自然数N=(p1n1) (p2n2)・・・(prnr)
(ただし、p1≠p2≠…≠pr)と因数分解できたとき、1からNまでの範囲で、
Nと互いに素の数の個数φ(N)(オイラー関数)は、
φ(N)=N(1-1/p1)(1-1/p2)・・・(1-1/pr)
で表される。この証明に、先ほどの包除の原理が利用できる。

| NO.956 | 2001.5.1. | 水の流れ | 不合格者は何人?(1) |
太郎さんのクラスの人数は40人います。
国語、数学、英語の試験を実施した結果、国語の合格者は8人、
数学の合格者は12人、英語の合格者は10人で、3科目とも合格者は5人でした。
このとき、3科目とも不合格者は何人以上いるでしょうか。

| NO.957 | 2001.5.1. | 水の流れ | 兄弟姉妹(1) |
実は、いつも悩んでいる問題があります。
50人のクラスで、男の兄弟がいる人は33人、姉妹がいる人は27人である。このとき、次の問に答えよ。
問題1:1人っ子は何人以下である。
問題2:男の兄弟、姉妹ともにいる人は何人以上いる。
問題3:男の兄弟だけがいる人は少なくとも何人、多くて何人までいる。
問題4:姉妹だけいる人は何人以下である。

| NO.958 | 2001.5.1. | kiyo | 兄弟姉妹(2) |
問題1:1人っ子は何人以下である。
0人以上、16人以下。
問題2:男の兄弟、姉妹ともにいる人は何人以上いる。
10人以上、26人以下。
問題3:男の兄弟だけがいる人は少なくとも何人、多くて何人までいる。
7人以上、23人以下。
問題4:姉妹だけいる人は何人以下である。
1人以上、17人以下。
LET XMAX=0
LET XMINI=50
LET YMAX=0
LET YMINI=50
LET ZMAX=0
LET ZMINI=50
LET SMAX=0
LET SMINI=50
FOR X=0 TO 33
FOR Z=0 TO 27
FOR Y=0 TO 27
IF X>0 AND Z>0 THEN
FOR S=0 TO 50
LET XY=X+Y
IF XY=33 THEN
LET YZ=Y+Z
IF YZ=27 THEN
LET T=X+Y+Z+S
IF T=50 THEN
IF XXMAX THEN
LET XMAX=X
END IF
IF YYMAX THEN
LET YMAX=Y
END IF
IF ZZMAX THEN
LET ZMAX=Z
EN D IF
IF SSMAX THEN
LET SMAX=S
END IF
END IF
END IF
END IF
NEXT S
END IF
NEXT Y
NEXT Z
NEXT X
PRINT XMINI;XMAX
PRINT YMINI;YMAX
PRINT ZMINI;ZMAX
PRINT SMINI;SMAX
END

| NO.959 | 2001.5.1. | kiyo | 不合格者は何人?(2) |
20人以上、 27人以下。
LET HMINI=40
LET HMAX=0
FOR A=0 TO 7
FOR B=0 TO 5
FOR C=0 TO 3
FOR D=0 TO 7
FOR E=0 TO 7
FOR F=0 TO 3
FOR G=5 TO 5
FOR H=0 TO 40
LET T=A+B+C+D+E+F+G+H
IF T=40 THEN
LET MA=A+D+E+G
IF MA=12 THEN
LET EN=B+E+F+G
IF EN=10 THEN
LET JA=C+D+F+G
IF JA=8 THEN
IF HHMAX THEN
LET HMAX=H
END IF
END IF
END IF
END IF
END IF
NEXT H
NEXT G
NEXT F
NEXT E
NEXT D
NEXT C
NEXT B
NEXT A
PRINT HMINI;HMAX
END

| NO.960 | 2001.5.2. | Junko | 当たりくじ(2) |
(1)問題1,2
どの箱を選ぶか、確率は1/nです。
k番目の箱を選んだとして、2本ともはずれの確率は、{(n-k)/n}2
従って、求める確率をP(n)とすると、
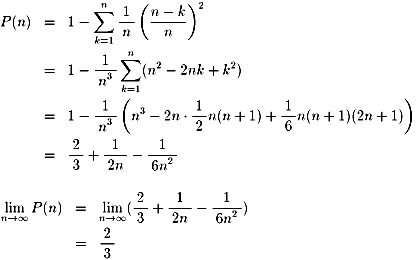
または、区分求積を用いて、
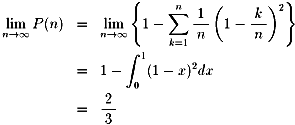

| NO.961 | 2001.5.2. | 与一 | 4桁の数字(1) |
ABCD×4=DCBAとなる4桁の数字がある。この4桁の数字を求めよ。

| NO.962 | 2001.5.2. | けんたん | 5×5の魔法陣 |
私が最近悩んでいる問題があります。魔法陣のことです。3×3の魔法陣は論
理的に作れるのに、5×5がどうしても作れません。よそのホームページで作り方を
教えてもらいましたが、どうしてその過程になるのかがわかりません。

 E-mail
E-mail
 戻る
戻る