Weekend Mathematics乛僐儘僉僂儉幒乛NO.112
僐儘僉僂儉幒
| NO.943
| 2001.4.1. | 彫愹丂廳晇 | 乽忣曬悽婭乿偺庡栶偨偪
|
懳悢偺儘僌俴倧倗偺岅尮傪偛懚偠偱偟傚偆偐丠
乽儘僑僗乿榑棟亄乽傾儕僗儉乿寁嶼亖乽儘僈儕僗儉僗乿懳悢偩偦偆偱偡丅
乽忣曬悽婭乿偺庡栶偨偪丅偲偄偆揥帵夛偺拞偵彂偄偰偁傝傑偟偨丅
乮
崙棫壢妛攷暔娰偺揥帵偺尦偵側偭偨僱乕僺傾偺杮偺儁乕僕乮嬥戲岺嬈戝妛強憼乯乯
崙棫壢妛攷暔娰
乮忋栰岞墍丄戝恖俉俁侽墌丄崅峑惗俀俆侽墌丅俇乛俁傑偱乯
忢愝揥偺嫄棾偺崪側偳傪尒傞偩偗偱傕壙抣偑偁傞偲巚偄傑偡偑丄
偙偺摿暿揥傪偪傚偭偲偺偧偄偰傒傞壙抣偼偁傞偲巚偄傑偡丅
僐儞僺儏乕僞乕偺榖偩偗偱偼側偔丄僷僗僇儖偺庤夞偟寁嶼婡傗丄僱乕僺傾偺懳悢昞丄弶傔偰
偺僥儗價曻憲偺條巕側偳傕揥帵偟偰偁傝傑偡丅

| NO.944
| 2001.4.2. | 悈偺棳傟 | 俀抜偵暲傋傞乮侾乯
|
戞俈俀夞悢妛揑側墳曞栤戣
懢榊偝傫偼丄庼嬈偺拞偱丄廲偑俀屄丄墶偑俀値屄偺彙栚偺偦傟偧傟偵愒偐敀偺儅僌僱僢僩傪暲傋傞偲偒偑偁傝傑偡丅
廲偵傕墶偵傕敀偺儅僌僱僢僩傪楢懕偟偰暲傋側偄曽朄偼壗捠傝偁傞偐丄抦傝偨偔側傝傑偟偨丅
廲偵俀屄丄墶偵俀値屄偺彙栚
| 丂 |
丂 |
丂 |
丂 |
| 丂 |
丂 |
丂 |
丂 |
偙偙偱丄栤戣偱偡丅
栤戣侾丗値亖侾偺偲偒丄偙偺傛偆側暲傃曽偼壗捠傝偁傞偐丅
栤戣俀丗値亖俀偺偲偒丄偙偺傛偆側暲傃曽偼壗捠傝偁傞偐丅
栤戣俁丗値亖俁偺偲偒丄偙偺傛偆側暲傃曽偼壗捠傝偁傞偐丅
栤戣係丗偙偺傛偆側俀抜偵暲傋傞応崌偺悢傪倎値偲偡傞偲偒丄
婯懃惈傪敪尒偟偰丄慟壔幃傪嶌偭偰偔偩偝偄丅
栤戣俆丗偙偺悢楍乷倎値乸偺堦斒崁傪値偱昞偟偰偔偩偝偄丅丂

丂
| NO.945
| 2001.4.3. | Junko | 俀抜偵暲傋傞乮俀乯
|
俀亊俀値側偺偐丄俀亊値丂側偺偐崿棎偟傑偟偨偗傟偳丄偙偙偱偼俀亊値偲偟偰峫偊偰傒傑偡丅
栤戣侾丗俁捠傝
栤戣俀丗俈捠傝
栤戣俁丗侾俈捠傝
崿棎偺偝側偐丄俀亊係傕彂偒弌偟偰傒傑偟偨偺偱嵹偣傑偡丅係侾捠傝丅
栤戣係丗
倎値亖倐値亄們値偲偡傞丅
(偨偩偟倐値偼丄塃抂偑僞僥偵愒敀丄傑偨偼敀愒偱廔傢傞傕偺丄
們値偼丄塃抂偑僞僥偵愒愒偱廔傢傞傕偺)
偦偆偟傑偡偲丄師偺慟壔幃偑惉傝棫偪傑偡丅
| 倐値 | 亖倐値亅侾 | 亄俀們値亅侾
|
| 們値 | 亖倐値亅侾 | 亄們値亅侾
|
側偤側傜丄塃抂偑僞僥偵愒敀傑偨偼敀愒偱廔傢傞偨傔偵偼丄慜抜偱愒敀傑偨偼敀愒偩偭偨応崌偼偦偺媡丄
慜抜偱愒愒偩偭偨応崌偼愒敀傑偨偼敀愒偺俀捠傝偑峫偊傜傟傑偡丅
乮倐値亖倐値亅侾亄俀們値亅侾乯
傑偨丄塃抂偑僞僥偵愒愒偱廔傢傞偨傑偵偼丄慜抜偑壗偱偁偭偰傕偐傑傢側偄偺偱偡丅
乮們値亖倐値亅侾亄們値亅侾乯
偙偙傑偱偺偲偙傠傪妋擣偟傑偡丅
倐侾亖俀丄們侾亖侾丄倎侾亖俀亄侾亖俁
倐俀亖俀亄俀丒侾亖係丄們俀亖俀亄侾亖俁丄倎俀亖係亄俁亖俈
倐俁亖係亄俀丒俁亖侾侽丄們俁亖係亄俁亖俈丄倎俁亖侾侽亄俈亖侾俈
倐係亖侾侽亄俀丒俈亖俀係丄們俀亖侾侽亄俈亖侾俈丄倎係亖俀係亄侾俈亖係侾
栤戣俆
慟壔幃偐傜堦斒夝傪媮傔偰傒傑偡丅
峴楍傪巊偭偰媮傔傞曽朄丄
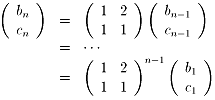
戙擖偡傞偙偲偱丄俁崁娫偺慟壔幃偵婣拝偝偣傞曽朄丄
俠値亄侾亅俀俠値亅俠値亅侾亖侽丂摍乆丒丒丒
偙偙偱偼搑拞傪徣棯偝偣偰偄偨偩偒傑偡丅寢壥偺傒丅
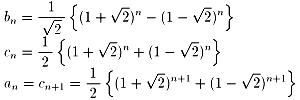
奺崁偼摉慠帺慠悢側偺偵丄堦斒崁偑偙傟偩偗暋嶨偲偄偆偺傕晄巚媍偲偄偊偽晄巚媍丒丒丒丅
傕偟丄俀亊俀値偱峫偊傞偺側傜偽丄忋婰偺値傪俀値偱抲偒捈偣偽偄偄傢偗偱丄偦偆偡傞偲埲壓偺傛偆偵側傝傑偡丅

戞俈俁夞慖敳崅峑栰媴戝夛乮枅擔怴暦幮丄擔杮崅峑栰媴楢柨庡嵜乯偺桪彑愴偑偁傝丄
忢憤妛堾乮堬忛乯偑愬戜堢塸乮媨忛乯傪俈懳俇偱攋傝弶桪彑傪壥偨偟偨丅
侾俋俋係擭偵弨桪彑偡傞側偳嫮崑偱丄俆夞栚偺僙儞僶僣弌応偱丄斶婅傪払惉偟丄
俀侾悽婭弶偺巼嵁偺桪彑婙偼忢憤妛堾乮栘撪娔撀乯偵搉傝傑偟偨丅偍傔偱偲偆偛偞偄傑偡丅
崱夞丄俀侾悽婭榞偑偁偭偰丄壂撽導偺媂栰嵗崅峑偲暉搰導偺埨愊崅峑偺俀峑憹偊偰偄傑偡丅
懢榊偝傫偼丄慜夞偺係夞偲摨條側挷嵏寢壥傪曬崘偟傑偡丅
偝偰丄崅峑栰媴偼愭庢揰偺擖偭偨僥乕儉偑彑偮偲傛偔尵傢傟傑偡丅
2001擭僙儞僶僣傪椺偵偟偰丄暘愅偟傑偟偨丅
傑偨丄僼傽儞偵偲偭偰丄媡揮偵偮偖媡揮偺帋崌偼朰傟傜傟側偄姶摦傪梌偊傑偡丅
乮侾乯愭庢揰偑擖偭偰丄摨揰偵偝傟偰傕偦偺傑傑廔傢偭偨帋崌傪嘆
乮俀乯愭庢揰偑擖偭偰丄媡揮偟偰乮摨揰偵側偭偰傕乯廔傢偭偨帋崌傪嘇
乮俁乯愭庢揰偑擖偭偰丄媡揮偝傟偰傕嵞媡揮偟偰廔傢偭偨帋崌傪嘊
埲壓丄偙偺媡揮偺夞悢偱丄嘋丄嘍丄嘐偲暘椶偟偰偄偒傑偡丅
偩偐傜丄娵悢帤偑婏悢偺応崌偼愭庢揰偺擖偭偨僠乕儉偑彑偪丅
娵悢帤偑嬼悢偺応崌偼愭庢揰偺擖偭偨僥乕儉偺晧偗丅偲側傝傑偡丅
摉慠丄娵悢帤偺懡偄曽偑柺敀偄帋崌偱妝偟傓偙偲偑偱偒偨偙偲偵側傝傑偡丅
寛彑愴傑偱偺俁俁帋崌傪偙偺傛偆偵暘愅偟傑偟偨丅
偦偺寢壥丄嘆偼俀侾帋崌丄嘇偼俋帋崌丄嘊偼俁帋崌丄偁偲偺夞悢偼婲偒傑偣傫偱偟偨丅
偦偙偱丄娵悢帤偺婏悢偼丂俀侾亄俁亖俀係丂丄娵悢帤偺嬼悢偼丂俋丂偩偗偱偡丅
偙傟傪俁俁偱妱傞偲俀係乛俁俁亖侽丏俈俀俈丂偱崅偄妋棪偱彑偭偰偄傑偡丅
偙傟偱丄僕儞僋僗偼妋偐偩尵偊傑偡丅
傑偨丄偙偺娵悢帤偺寛傑偭偨僀僯儞僌偼侾夞偐傜俁夞偱侾俆帋崌偙偺偆偪嘆偺僠乕儉偑
侾係僠乕儉偁傝傑偡丅
係夞偐傜俇夞偱俋帋崌丄俈夞偐傜俋夞偱俇帋崌丄墑挿愴偺応崌偑係帋崌偱丄
僒儓僫儔彑偪偼俁帋崌偱偟偨丅
傑偨丄偙偺僙儞僶僣戝夛偼丄愭峌傪偲偭偰彑偭偨帋崌偑侾俆帋崌丄
屻峌偑彑偭偨帋崌偑侾俉帋崌偁傝傑偟偨丅
偝偰丄偙偙偱丄偄偮傕摨偠傛偆偵丄栰媴偺帋崌傪峴偭偨偲偒
乽俋夞棤乮墑挿乯傑偱偺偁偄偩偵媡揮傑偨偼彑偪墇偟偑壗夞婲偙傞偐乿偲尵偆昿搙偑丄
乭傑傟偵偟偐婲偙傜側偄偙偲乭偺侾椺偱偡丅
愭惂揰傪嫇偘偨僠乕儉偑偦偺傑傑摝偘愗偭偰偟傑偊偽丄
侾夞傕媡揮丄彑偪墇偟偑側偐偭偨偙偲偵側傞丅
偦偙偱丄椺偲偟偰丄戝夛弶擔偺暉堜彜嬈崅峑偲嶗旤椦偲偺摼揰宱夁偱傒傑偡丅
| 摼揰宖帵 | 侾 | 俀 | 俁 | 係
| 俆 | 俇 | 俈 | 俉 | 俋 | 寁 |
|---|
| 暉堜彜嬈 | 侾 | 侾 | 俀 | 俀
| 侽 | 侽 | 侽 | 侽 | 俆 | 侾侾 |
|---|
| 嶗旤椦 | 侾 | 侾 | 侽 | 侽
| 侾 | 係 | 侾 | 侾 | 侽 | 俋 |
|---|
侾夞偺昞偺侾揰偼愭惂揰偩偐傜丄彑偪墇偟偲偼尵傢側偄丅侾夞偺棤偺侾揰偼摨揰偩偐傜僇僂儞僩偟側偄丅
俀夞偺昞偺侾揰偼彑偪墇偟偩偐傜丄僇僂儞僩偼侾偲偟傑偡丅
俀夞偺棤偺侾揰偼摨揰偩偐傜僇僂儞僩偟側偄
俁夞偺昞偺俀揰偼彑偪墇偟偩偐傜丄僇僂儞僩偼俀偲偟傑偡丅
俇夞偺棤偺係揰偼彑偪墇偟偩偐傜僇僂儞僩俁偟傑偡
俋夞偺昞偺俆揰偼嵞媡揮偱偡偺偱丄僇僂儞僩係偟傑偡
埲忋丄媡揮傑偨偼彑偪墇偟偑夞悢偲偟偰係夞傪僇僂儞僩偟傑偡丅
偙偺帋崌偑摦偒偺寖偟偄帋崌偱偁偭偨偙偲傪堄枴偟偰偄傑偡丅
摨偠傛偆偵僇僂儞僩係偺帋崌偼丄昉楬岺嬈崅峑偲擔戝嶰崅偲偺帋崌傕俆懳俉偱丄
媡揮丒嵞媡揮丒嵞乆媡揮偺岲帋崌偱偟偨丅
媡揮丒彑偪墇偟偑婲偭偨夞悢
| 夞悢 | 俀侽侽侾擭弔偺僙儞僶僣 | 俀侽侽侾擭壞偺戝夛
|
|---|
| 侽夞 | 侾係帋崌 | 丂
|
| 侾夞 | 侾俁帋崌 | 丂
|
| 俀夞 | 丂係帋崌 | 丂
|
| 俁夞 | 丂侽帋崌 | 丂
|
| 係夞 | 丂俀帋崌 | 丂
|
忋偺昞偑億傾僜儞暘晍傪偟偰偄傞偐傪傒偰傒傑偡丅
偪傚偭偲丄悢妛偺愱栧揑側幃偵側傝傑偡偑丄億傾僜儞暘晍偺妋棪枾搙娭悢偼
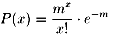 丂丂偱偡丅
丂丂偱偡丅
偙偙偱丄倶偼媡揮傑偨偼彑偪墇偟偺夞悢傪戙擖丄倣偼僨乕僞偺暯嬒抣偱丄偙偺応崌偼
倣亖乮侾亊侾俁亄俀亊係亄俁亊侽亄係亊俀乯乛俁俁亖俀俋乛俁俁亖侽丏俉俈俉俈乧
偙傟偼丄偙偺擭偺僙儞僶僣偱偼丄媡揮傑偨偼彑偪墇偟偑侾帋崌暯嬒侽丏俉俈俉俈夞
婲偙偭偨偙偲傪堄枴偟偰偄傑偡丅堄奜偵彮側偄偲姶偠傑偟偨丅挷嵏偟偰偄傞偲摨偠傛偆側寢壥偵側傝丄
壞偺戝夛傛傝丄偙傟偱傕懡偄曽偱偡丅
| 媡揮丒彑偪墇偟偑婲偙傞妋棪 | 棟榑抣 | 幚嵺偺帋崌悢
|
|---|
| 侽夞丂侽丏係侾俆俁亊俁俁 | 侾俁丏俈侽係 | 侾係
|
| 侾夞丂侽丏俁俇係俋亊俁俁 | 侾俀丏侽係俁 | 侾俁
|
| 俀夞丂侽丏侾俇侽係亊俁俁 | 丂俆丏俀俋俀 | 丂係
|
| 俁夞丂侽丏侽係俈侽亊俁俁 | 丂侾丏俆俆侽 | 丂侽
|
| 係夞丂侽丏侽侾侽俁亊俁俁 | 丂侽丏俁係侾 | 丂俀
|
埲忋丄俆夞栚偺挷嵏曬崘偱偟偨丅

| NO.947
| 2001.4.5. | kiyo | 俀抜偵暲傋傞乮俁乯
|
2n偺応崌偼埲壓偺傛偆偵側傞偲巚偄傑偡丅
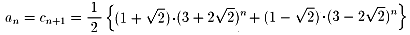

| NO.948
| 2001.4.5. | Junko | 俀抜偵暲傋傞乮係乯
|
傢偀乕丄杮摉偩丄寁嶼娫堘偄偟偰偄傑偡偹丅偛巜揈丄偁傝偑偲偆偛偞偄傑偡丅

| NO.949
| 2001.4.15. | 悈偺棳傟 | 嵟戝悢偺妋曐
|
戞俈俁夞悢妛揑側墳曞栤戣
懢榊偝傫偼丄偲偒偳偒戝妛擖帋栤戣傪尒偰偄傑偡丅
夁嫀偺憗堫揷戝妛偺擖帋栤戣傪嶲峫偵偟偰嶌栤偟傑偡丅
乽値傪俀埲忋偺帺慠悢偲偟丄師偺憖嶌傪峫偊傞丅
亀憖嶌侾亁丗侾偐傜値傑偱偺帺慠悢傪侾枃偢偮彂偄偨値枃偺嶥傪柍嶌堊偵侾楍偵暲傋傞丅
亀憖嶌俀亁丗侾枃栚偺嶥傪庤尦偵庢傞丅
亀憖嶌俁亁丗俀枃栚埲崀丄値枃栚偺嶥傑偱弴偵尒偰偄偒丄
庤偵偟偰偄傞嶥傛傝傕偦傟偑戝偒偄悢抣偺嶥偱偁傞側傜偽丄偦偺偨傃偵庤偺嶥偲擖傟姺偊傞丅
偙偺偲偒丄亀憖嶌俁亁偱擖傟姺偊偑倠夞婲偒傞暲傃曽偺悢傪俥乮値丄倠乯偲偡傞丅
偨偩偟丄嵟弶偵庤偵偟偨侾枃偺嶥偼憖嶌偺夞悢偲偟偰偼丄侽夞偲偟傑偡丅
傑偨丄俥乮侾丄侽乯亖侾偲偟傑偡丅乿
椺偊偽丄俆枃偺嶥偑俀丆侾丆俁丆俆丄係偲侾楍偵暲傫偩偲偟傑偡丅
嵟弶偵俀傪庤尦偵擖傟傑偡丅師偺侾偼俀傛傝戝偒偔偁傝傑偣傫偐傜丄
擖傟懼偊偺憖嶌偼偟側偄丅師偺俁偼庤偵偟偰偄傞俀偺嶥偲斾傋偰戝偒偄悢偱偡偐傜丄
侾夞栚偺擖傟姺偊憖嶌傪偟傑偡丅
偦偟偰丄俆偺嶥偑暲傫偱偄傑偡偐傜丄俀夞栚偺擖傟姺偊憖嶌傪偟傑偡丅
偙偺応崌偼丄倠亖俀偺暲傃曽偺侾椺偱偡丅偙偙偐傜丄栤戣偱偡丅
栤戣侾丗俥乮俀丄侽乯丄俥乮俀丄侾乯偺抣傪媮傔偰偔偩偝偄丅
栤戣俀丗俥乮俁丄侽乯丄俥乮俁丄侾乯丄俥乮俁丄俀乯偺抣傪媮傔偰偔偩偝偄丅
栤戣俁丗俥乮係丄侽乯丄俥乮係丄侾乯丄俥乮係丄俀乯丄俥乮係丄俁乯偺抣傪媮傔偰偔偩偝偄丅
栤戣係丗俥乮俆丄侽乯丄俥乮俆丄侾乯丄俥乮俆丄俀乯丄俥乮俆丄俁乯丄俥乮俆丄係乯偺抣傪媮傔偰偔偩偝偄丅
栤戣俆丗婯懃惈傪敪尒偟偰丄慟壔幃傪媮傔偰偔偩偝偄丅
栤戣俇丗擖傟姺偊偺夞悢偺婜懸抣傪俤乮値乯偲偟偨偲偒丄
俤乮値乯偲俤乮値乗侾乯偺娫偵惉傝棫偮娭學幃傪傒偮偗偰丄俤乮値乯傪値偱昞偟偰偔偩偝偄丅

| NO.950
| 2001.4.24. | Junko | 嵟戝悢偺妋曐乮俀乯
|
椺偵傛偭偰傑偢偼悢偊忋偘丒丒丒
栤戣侾丗
俥乮俀丄侽乯亖侾丂丂側偤側傜丄[俀丆侾]
俥乮俀丄侾乯亖侾丂丂側偤側傜丄[侾丆俀]
栤戣俀丗
俥乮俁丄侽乯亖俀丂丂側偤側傜丄[俁丆仏丆仏]丒丒丒仏偼巆傝偺擟堄偺悢
俥乮俁丄侾乯亖俁丂丂側偤側傜丄[侾丆俁丆俀]丄[俀丆俁丆侾]丄[俀丆侾丆俁]
俥乮俁丄俀乯亖侾丂丂側偤側傜丄[侾丆俀丆俁]
栤戣俁丗
俥乮係丄侽乯亖俇丂丂側偤側傜丄[係丆仏丆仏丆仏]丒丒丒仏偼巆傝偺擟堄偺悢
俥乮係丄侾乯亖侾侾丂側偤側傜丄[侾丆係丆俀丆俁]丄[侾丆係丆俁丆俀]丄[俀丆係丆侾丆俁]丄[俀丆係丆俁丆侾]
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂[俁丆係丆侾丆俀]丄[俁丆係丆俀丆侾]
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂[俀丆侾丆係丆俁]丄[俁丆侾丆係丆俀]丄[俁丆俀丆係丆侾]
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂[俁丆侾丆俀丆係]丄[俁丆俀丆侾丆係]
俥乮係丄侾乯亖俇丂丂側偤側傜丄[侾丆俀丆係丆俁]丄[侾丆俁丆係丆俀]丄[俀丆俁丆係丆侾]
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂[侾丆俁丆俀丆係]丄[俀丆俁丆侾丆係]丄[俀丆侾丆俁丆係]
俥乮係丄侾乯亖侾丂丂側偤側傜丄[係丆俀丆俁丆係]
栤戣係丗
俥乮俆丄侽乯亖俀係丂側偤側傜丄[俆丆仏丆仏丆仏丆仏]丒丒丒仏偼巆傝偺擟堄偺悢
俥乮俆丄侾乯亖俆侽
偙偺偁偨傝偱悢偊忋偘偼嵙愜丒丒丒丅
慟壔幃傪峫偊偨曽偑傛偝偦偆偱偡丅
偙偙傑偱偱傢偐偭偨惈幙偼丄
F(n,1)=(n-1)!丒丒丒側偤側傜愭摢偵値偑偒偰巆傝偼擟堄偺悢偱偄偄偐傜
F(n,n-1)=1丒丒丒彫偝偄弴偵暲傋偰偍偔埲奜偵偼側偄偐傜
F(n,0)+F(n,1)+丒丒丒+F(n,n-1)=n!丒丒丒偡傋偰偺榓偼丄値偙偺悢帤偺弴楍偩偐傜

| NO.951
| 2001.4.26. | 恄屗戝妛偺S.N | 榓廤崌偺梫慺偺屄悢乮俀乯
|
n屄偺榓廤崌偺梫慺偺屄悢傪媮傔傞偙偲偑偱偒傞堦斒岞幃傪嫵偊偰偔偩偝偄丅
俀屄丄俁屄偺応崌[n(A伾B乯亖n乮A)+n乮B)-n乮A伻B乯摍]偐傜摢偺拞偱偼悇應偱偒傞偺偱偡偑丄
幃偑戝曄側検偵側偭偨傝丄
僔僌儅婰崋偑暋嶨偵廳側傝崌偭偨傝偲忋庤偵傑偲傔傞偙偲偑弌棃傑偣傫偱偟偨丅
乽偙偺堦斒岞幃傪悇應偟偰丄悢妛揑婣擺朄偱徹柧偣傛丅乿偲偄偆偺偑栤戣側偺偱偡偑丄
偤傂堦斒岞幃偩偗嫵偊偰偔偩偝偄丅傛傠偟偔偍婅偄偟傑偡丅丂丂

| NO.952
| 2001.4.27. | Kernighan | 榓廤崌偺梫慺偺屄悢乮俀乯
|
巹偼嵟嬤抦傝傑偟偨丅
曪彍尨棟
X伣{Pi}丂丂i=1,2,3...,n 偵懳偟偰
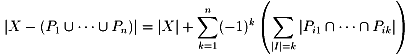
偨偩偟I={i1,...,ik}
椺偊偽n=2偺応崌偼
|X-(P1伨P2)|=|X|-(|P1|+|P2|)+|P1伩P2|
n=3偺応崌偼
|X-(P1伨P2伨P3<)|=|X|-(|P1|+|P2|+|P3|)+
(|P1伩P2|+|P2伩P3|+|P3伩P1|)-|P1伩P2伩P3|
偙傟傪巊偭偰僆僀儔乕娭悢傗丄憃巕慺悢偺僽儖儞偺饪傪峔惉偱偒傑偡丅

 E-mail
E-mail
 栠傞
栠傞



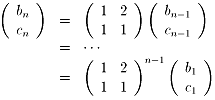
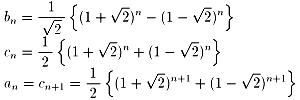
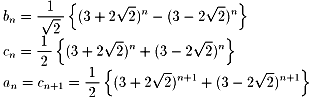

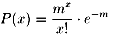 丂丂偱偡丅
丂丂偱偡丅
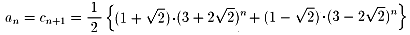





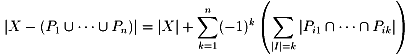

 E-mail
E-mail
 栠傞
栠傞