
Weekend Mathematics/コロキウム室/NO.110
| NO.933 | 2001.2.4. | 水の流れ | 3の倍数(1) |
太郎さんは、先日1年生対象に実力テスト問題を作りました。
そこで、同じような問題を作りました。
数字1,2,3,4,5,6,7,8,9の9個から異なるk個の整数を選んで並べた
k桁の整数を作ったとき、
次のように桁数に応じて、3の倍数ができる確率を求めよ。
問題1:k=1、2、3のとき、
問題2:k=4,5,6のとき、
問題3:k=7,8,9のとき
問題4:何か発見できたことを教えてください。
問題5:トランプのダイヤのカード13枚
(ただし、J、Q、Kは11,12,13と考える)から、同時に3枚を取り出すとき、
その3枚のカードの和が13の倍数になる確率を求めよ。
(ヒント:問題4で発見したことを利用すると鮮やかに解けます。
勿論、場合分けしても良いです。)

| NO.934 | 2001.2.15. | かつ | 箱の問題・その後(7) |
5つのコンパスのみによる作図ですが、
一応こうやるとコンパスのみで作図することができます。
それでは順にやっていきましょう。
1.直線上の任意の点が取れることと言い換えました。
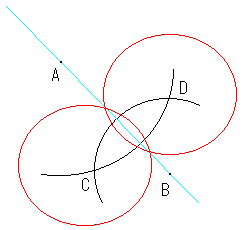
これは比較的簡単にできると思います。
AB上に無い点Cを任意に取り、ABに関して対称な点Dをとります。
これはできるでしょう。後は、点C、Dから同じ長さの半径で書けばAB上の点となります。
この半径の長さを換えることによって、AB上の任意の点をとることができます。
2.3.は省略します。
4.与えられた円と与えられた2点で定まる直線との交点を求める。
これは2点が円上に無いこととします。
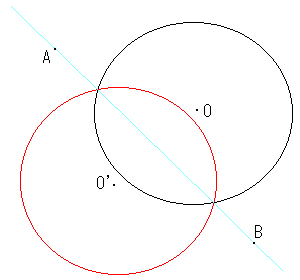
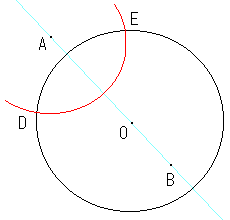
5.それぞれ与えられた2点で定まる2つの直線の交点を求める。
2つの直線をAB、CDとします。ちなみに平行ではない。
C、DのABに関して対称な点をC1、D1とします。D1中心、
半径CC1の円とD中心CD半径の円の交点をEとします。
最後にDE:DD1=CD:DXとなるようにXをとるとXが求める点。
ここに書いた書き方ではまだ2か所ほど求められないと思います。
とても書きにくいので後に回したいと思います。
4.5はそのときに改めて載せた方が良いと思われます。
最後にある本にこんなことが載っていました。
「コンパスと定木によってできるすべての作図問題は、
その図の平面内に1つの定円とその中心が与えられれば、定木だけで解くことができる。」
ということです。
世の中にはできないと思うようなことでも、不思議とできてしまうことがあるのですね。
常識が覆された感じがします。

| NO.935 | 2001.2.18. | 水の流れ | インフィールド・ライン(1) |
先日、太郎さんは、勤務している硬式野球の監督から、 「野球競技場の内野に書いてあるインフィールドライン(扇形の円弧)の長さを知りたいので、 求めていただけませんか」を課題をもらいました。誰か教えてください。図の青の円弧の長さです。
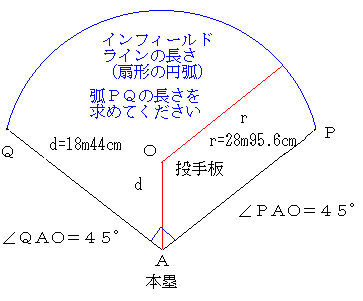

| NO.936 | 2001.2.19. | Junko | 3の倍数(2) |
数字1,2,3,4,5,6,7,8,9の9個から異なるk個の整数を選んで並べた
k桁の整数を作ったとき、3の倍数ができる確率をP(k)とします。
問題1〜4:
ある自然数が3の倍数かどうかということは、
各桁の数字をたして3の倍数になるかどうかということと同値です。
従ってこの問題は、1〜9までの9個の数字の中から同時
にk個の数を取り出し、その和が3の倍数となっている確率を出せということになります。
対称性から、この確率はすべて1/3なのでしょうか?
でも少なくとも、P(9)=1ですよね・・・。
これは1〜9までのすべての数を選ぶ以外にないわけですから、確実に3の倍数です。
もう少し調べてみましょう。
ここで、1〜9までの数を3による剰余類に分類しましょう。
0={3,6,9}
+={1,4,7}
−={2,5,8}とします。
やはりすべて1/3なんて、単純ではありませんでした。
以下同様に調べてみます。
問題5:
対称性を考慮すると、確率はP=1/13のようにも思います。
13の倍数として考えられるのは、13と26です。
すべて数え上げてみました。
| 和が13 | 和が26 | |||||
| {1,2,10} | {1,3,9} | {1,4,8} | {1,5,7} | {1,12,13} | ||
| {2,3,8} | {2,4,7} | {2,5,6} | {2,11,13} | |||
| {3,4,6} | {3,10,13} | {3,11,12} | ||||
| {4,9,13} | {4,10,12} | |||||
| {5,8,13} | {5,9,12} | {5,10,11} | ||||
| {6,7,13} | {6,8,12} | {6,9,11} | ||||
| {7,8,11} | {7,9,10} |

| NO.937 | 2001.2.21. | Junko | インフィールド・ライン(2) |
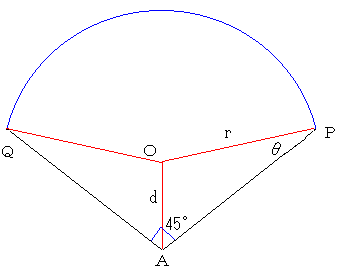
インフィールドラインは、投手板を中心とした扇形の円弧ととらえます。
∠APO=θとし、△AOP(or△AOQ)において余弦定理を使うと、
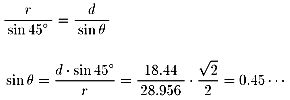
これより、θ≒27゚
従って、∠POQ≒(45゚+27゚)×2=144゚
弧PQ=2πr×(144/360)≒72.74・・・(m)

 E-mail
E-mail
 戻る
戻る