ここで次の疑問が沸いて来ました.
放物線(2)の下の部分で,円(1)の内部も,やはり囲まれる部分としていいのではないか?
したがって答は円の内部および周ではないか?
Weekend Mathematics/コロキウム室/NO.108
| NO.921 | 2001.1.9. | 浜田 明巳 | 囲まれる部分 |
同僚が次の疑問に悩んでいました.紹介します.
高崎経済大学の入試問題です.
次の2つのグラフによって囲まれる部分を示せ.
x2+y2=1………(1)
y=x2−1/4……(2)
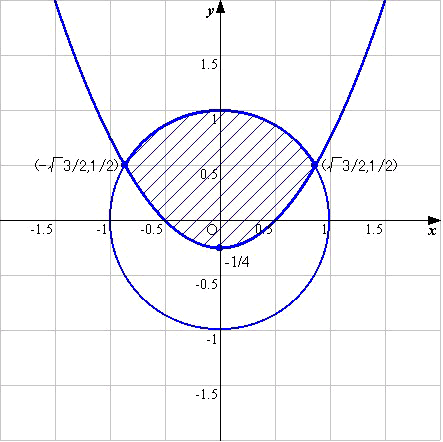
模範解答は下図の通りで,
x2+y2≦1
y≧x2−1/4
の2つの不等式で表される領域です.

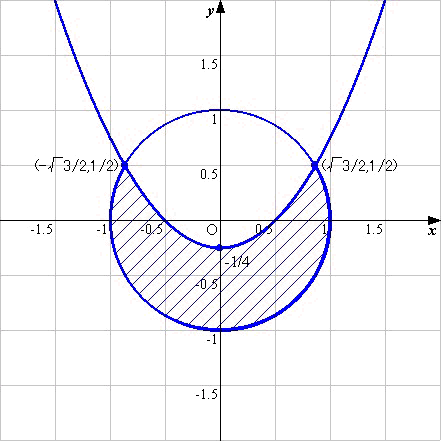
ここで次の疑問が沸いて来ました.
放物線(2)の下の部分で,円(1)の内部も,やはり囲まれる部分としていいのではないか?
したがって答は円の内部および周ではないか?
おそらくこれは,「放物線(2)で囲まれる」ということから,常識的(?)に,
その放物線の開いている部分,この場合では,上の部分内でのみ考えてしまったので,
起きた事柄なのでしょう.
問題自体に問題があるので,あまり気にしなくてもいいのかも知れません.
しかし作問者,採点者,受験生のほとんどが最初の図を,
何も考えず答とする一方,小数の受験生が2番目の図でもいいのではないか,と悩むのは問題です.
かわいそうです.
こういう場合,数学の先生として,どう指導していけばいいのでしょうか.
実際の入試では,あまり冒険せず,「変だな」と思っても常識的な考えで行け,
と指導しようと思ってはいるのですが.

| NO.922 | 2001.1.10. | Junko | インド工科大学入試問題(2) |
1.についてです。
解と係数の関係を使って証明すればいいのかとも思いますが、
証明すべき式の両辺の形、まったく同じ形をしているのが気になります。
つまり2つの解が、δだけずれたとしても不変な量だということです。
何かきっと意味があるに違いないと思うわけです。
2次方程式の解の公式を
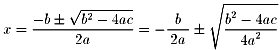 と変形します。
と変形します。
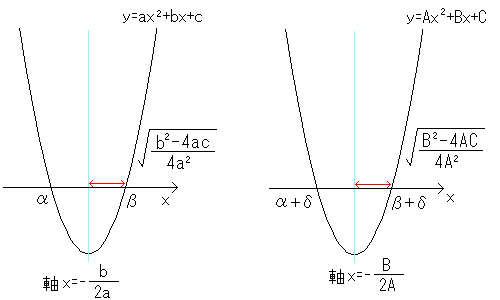
α<βとするならば、
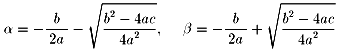
であり、放物線の軸 x=-b/2a をはさんで左右対称です。
従って、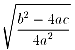 は、
放物線の軸とx軸との交点と、放物線とx軸との交点との距離(下の図の赤い部分)を示しています。
は、
放物線の軸とx軸との交点と、放物線とx軸との交点との距離(下の図の赤い部分)を示しています。
この長さは、グラフ全体を右にδだけずらしても変わらないわけですから、
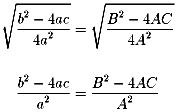 (証明終わり)
(証明終わり)

| NO.923 | 2001.1.10. | qthuman | プレゼントの問題(17) |
(一部訂正1/12)
プレゼント交換の問題で少し加わった問題がありました。
円卓に8人座っています。この8人でプレゼント交換するのです
が、自分のプレゼントはもらうことはできず、しかも右隣の人に渡す事ができないとします。
このとき何通りの交換の仕方があ
るでしょう。
また一般的にn人の場合についてはどうでしょう。

| NO.924 | 2001.1.14. | Chikako | ボ−ルの問題・その後(2) |
ボールの問題、結局わかりました。
やはり、3回でわかるのです。
まず、12個のボールを4個ずつ3このグループにわける。
(説明のため、ABCD、EFGH、IJKLの名前を付けておきます。)
最初に、ABCD、EFGHをはかりに乗せる。

| NO.925 | 2001.1.14. | かつ | 箱の問題・その後(5) |
今回は正17角形が作図できることについてです。
正17角形だけでなくある規則に沿って正確な作図ができる正n角形が存在するそうです。
「nを素因数分解したとき、その奇数の因数がすべてフェルマー素数であり、同じものが2つ以上無い場合に限り定規とコンパスによって作図することができる。」
というのをガウスが証明したそうです。
ということで結局n=100までで、正確な作図可能な正n角形は、24種類ということになるそうです。

| NO.926 | 2001.1.14. | 水の流れ | お年玉2 |
太郎さんは、高いところからひらひらと舞い降りてくる幾つかの1万円札をうまく割り箸
でつかみ取ることができたら、その分をお年玉としてゲットできる番組を観ていました。
そこで、n枚の1万札をr人(ただし、nとrは自然数とする)でつかみ取る問題を作りました。
勿論、1人が運良くすべての札をゲットしたり、すべての人が運悪く1枚もゲット
できないときもあります。
具体的には
問題1:5枚の1万札を3人でチャレンジしてつかみ取る方法は何通りですか。
問題2:n枚の1万札を3人でチャレンジしてつかみ取る方法は何通りですか。
問題3:5枚の1万札をr人でチャレンジしてつかみ取る方法は何通りですか。
問題4:n枚の1万札をr人でチャレンジしてつかみ取る方法は何通りですか。

| NO.927 | 2001.1.14. | 水の流れ | お年玉(4) |
私も同じように多項式を展開した係数で求めることを考えました。
問題3を考えてみます。
1万円札3枚をa、a、a、5千円札2枚をb、b、2千円札2枚をc、cとすると、
ここから、n(n=1から7までの自然数)個を選んで、並べる方法の数です。
ここで、n!(1+x+x2/2!+x3/3!)(1+x+x2/2!)(1+x+x2/2!)
という多項式を考えます。
ここで、n=5を考えてみます。計算は「Mathematica」にしてもらいました。
| 与式 | ={5!÷(3!2!2!)}×(6+6x+3x2+x3)(2+2x+x2)2 |
| =120+360x+540x2+500x3+540x4+130x5+35x6+5x7 |

| NO.928 | 2001.1.15. | 浜田 明巳 | インド工科大学入試問題(3) |
1.について
ax2+bx+c=0(a≠0)
の1解がαなので,
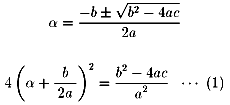
解と係数の関係から,
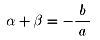
(1)に代入すると,
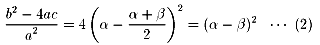
同様に,
Ax2+Bx+C=0(A≠0)
の2解がα+δ,β+δなので,
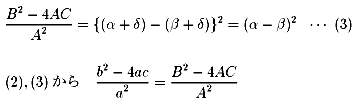

| NO.929 | 2001.1.16. | Junko | インドの数学事情(2) |
インドの数学事情についての記事はこちら
AERA 2000年12月25日号

| NO.930 | 2001.1.19. | かつ | 箱の問題・その後(6) |
箱のところで
「コンパスと定木でできる作図はすべてコンパスのみで作図できる。」
というのがありました。
それについて、以下のことがわかればいいと思います。
この作図は置いておいて、今は直線ABをn等分をコンパスのみで作図します。
まず、ABをn倍します。正三角形を作る要領で、やっていきます。
つまり、3つの正三角形の頂点が集まると180度であるのでABの2倍の点が見つかります。
そこでn回繰り返すとABのn倍の点が見つかります。それをCとしておきましょう。
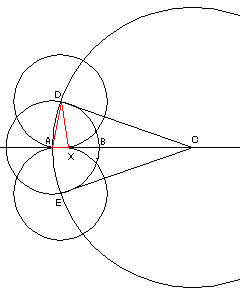
次に、長さACで中心Cの円を書き、長さAB中心Aの円との交点をD、Eとします。
最後にD、E中心で長さAD、AEの円を書き、交点をXとすると、
これはABの直線上にありAX=(1/n)ABとなります。
この証明は、ADCとAXDが相似であることからわかります。

 E-mail
E-mail
 戻る
戻る