
Weekend Mathematics/コロキウム室/2000.10〜12/NO.104
| NO.888 | 2000.11.10. | 水の流れ | ペル方程式の最小解(2) |
ペルの方程式は京都大学・お茶の水大学・東京女子大学の入試問題に
形を変えて出ていましたので、受験雑誌に解法が載っています。
x2=Dy2+1 (Dは平方数でない)の最小自然数は
手持ちの平方数表を見ながら、yに順次小さい数字を代入していくとでてきます。
D=2のとき、(3,2)
D=3のとき、(2,1)
D=5のとき、(9,4)
D=6のとき、(5,2)
D=7のとき、(8,3)
D=8のとき、(3,1)
D=10のとき、(19,6)
D=11のとき、(10,3)
D=12のとき、(7,2)
D=13のとき、(?,?)
D=14のとき、(15,4)
D=15のとき、(4,1)
D=17のとき、(33,8)
D=18のとき、(17,4)
D=19のとき、(?,?)
D=20のとき、(9,2)
D=21のとき、(55,12)
D=22のとき、(?,?)
D=23のとき、(24,5)
D=24のとき、(5,1)
D=26のとき、(51,10)
D=27のとき、(26,5)
D=28のとき、(?,?)
D=29のとき、(?,?)
D=30のとき、(11,2)
・・・・・

| NO.889 | 2000.11.10. | ねこ | ペル方程式の最小解(3) |
ペル方程式の最小解
ペル方程式の最小解はDと平方数との差に関係があります。
例えば、
D=k2−1のとき(k,1)
3(2,1)
8(3,1)
15(4,1)
24(5,1)
・・・・・・
D=k2+1のとき(2D−1,2k)
2( 3, 2)
5( 9, 4)
10(19, 6)
17(33, 8)
26(51,10)
・・・・・・
などです。ほかのDについてはどのような法則があるでしょうか?

| NO.890 | 2000.11.11. | 水の流れ | お祝い問題 (3) |
「お祝いの問題」 で、下記のようなパスカルの三角形みたいのが得られました。 ここで、コロキウムの「コ」と水の流れの「ミ」をとって、コミカルな三角形と呼びましょう。
| n | (1+x+x2)nの係数 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | ||||||
| 2 | 1 | 2 | 3 | 2 | 1 | ||||
| 3 | 1 | 3 | 6 | 7 | 6 | 3 | 1 | ||
| 4 | 1 | 4 | 10 | 16 | 19 | 16 | 10 | 4 | 1 |
| ・・・ | ・・・ | P(n、r) | |||||||
この数字をP(n、r)で表すことにします。
ただし、n=0,1,2,3,・・・・、0≦r≦2n とする。
また、P(n、0)=1、P(n、1)=n、P(n、2nー1)=n、P(n、2n)=1 とする。
すると、このコミカルの三角形は
P(n+1,r)= P(n,r−2)+P(n,r−1)+P(n,r) という性質を持っています。
これは、上の段の3つの和として、順に得られますので、トリボナッチ数列にもなります。

| NO.891 | 2000.11.13. | 水の流れ | 多項式展開係数(1) |
太郎さんは、先日生徒から「ニュートンの2項定理って、何ですか。」と聞かれました。
すぐには答えられませんでしたが、
パスカル(フランス:1623〜1662)の三角形が出てくる2項係数を思い出して、
(a+b)nの2項定理を言いました。ただし、このnは正の整数です。
しかし、ニュートン(イギリス:1642〜1727)と名前が出ているので、
2項定理の発見者はニュートンかしらと疑問に思っていました。そこで、文献で調べてみました。
文学、物理学、気象学の分野で多彩な業績を残したパスカルは、数学においても、
数多くの成果をあげています。転がる円盤の一点が描くサイクロイドの研究はや、
フェルマー(フランス:1601〜1665)と共同で行った確率の研究は、特に優れたものです。
パスカルは確率の研究から、2項式の展開(a+b)nにおいて、
係数の規則性を発見しました。
これが、これがいわゆるパスカルの三角形と言われる魔法の三角形です。
多くの人は、ものご存じですので、割愛します。1654年に発案しました。
実はこの三角形は中国で古くから知られていました。
朱世傑の著書で1303年頃書かれた「四元玉鑑」を見ると、
すでに2項展開したときの係数が書かれています。
これは、高次方程式を解くにあたって使用されていました。
また、ヨーロッパでも16世紀の数学者、カルダノ(イタリア:1501〜1576)らが知っていて、
3次行程式や4次方程式の解法に使ったいました。
弱冠23歳のニューートンが、1665年の初めに、
パスカルの発見した「2項定理」の指数nを拡張して、
正の整数から、負の整数、分数まで拡げ、無限級数にまで発展させている。
αが任意の実数のとき、(1+x)αをベキ級数に展開できる公式を
「ニュートンの2項定理」と言います。
この係数は組み合わせの記号C(n、r)と書きますが、
nが正整数でないと組み合わせの意味がなくなりますが、
n=α,r=nとして、2項係数は、
α(α-1)(α-2)(α-3)・・・(α-n+1)/n!={α,n}と表します。
例えば、α=−1のとき、1+x+x2+x3+x4+・・・+xn+・・・=1/(1−x)
となることです。
で、いろいろと文献を見て、次のような問題を考えてみました。
まず、3項式(1+x+x2)nの展開係数を見て下さい。
n=0,1,2,3,4,5,・・・と展開すると、パスカルの三角形は2項式(1+x)nの展開係数ですが、
似たような奇妙な数列がでてきます。一度見て下さい。
(この三角形をコミカルな三角形と呼びましょう。)
| n | (1+x+x2)nの係数 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | ||||||||
| 2 | 1 | 2 | 3 | 2 | 1 | ||||||
| 3 | 1 | 3 | 6 | 7 | 6 | 3 | 1 | ||||
| 4 | 1 | 4 | 10 | 16 | 19 | 16 | 10 | 4 | 1 | ||
| 5 | 1 | 5 | 15 | 30 | 45 | 51 | 45 | 30 | 15 | 5 | 1 |
| ・・・ | ・・・ | P(n、r) | |||||||||
この数字をP(n、r)で表すことにします。
ただし、n=0,1,2,3,・・・・、0≦r≦2n とする。
また、P(n、0)=1、P(n、1)=n、P(n、2nー1)=n、P(n、2n)=1 とする。
すると、このコミカルの三角形は
P(n+1,r)= P(n,r−2)+P(n,r−1)+P(n,r)
という性質を持っています。
これは、上の段の3つの和として、順に得られますので、トリボナッチ数列にもなります。
ここからが、今回の問題です。次の初項から第k項までの和をkで表してください。
問題1:T1=1+1+1+・・・+T0 (ただし、T0=1とする)
問題2:T2=1+2+3+4+・・・+T1
問題3:T3=1+3+6+10+・・・+T2
問題4:T4=1+4+10+20+・・・+T3
問題5:T5=1+5+15+35+・・・+T4
問題6:一般に、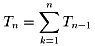
(n=1,2,3,・・・、ただし、T0=1とする)
さて、最後に問題7:
この展開を拡張して、多項式(1+x+x2+x3+x4+・・・)n
の展開係数を考えてください。

| NO.892 | 2000.11.14. | 水の流れ | 極方程式の微分 |
極方程式 r=f(θ)において、これを1回微分した導関数は一体何を意味しますか。
この極方程式で与えられた曲線の極値の求め方はどうするのでしょう。
また、2回微分した導関数は一体何を意味しますか。
この極方程式で与えられた曲線の凹凸の求め方はどうするのでしょう。

| NO.893 | 2000.11.23. | Junko | 多項式展開係数(2) |
この数列は2変数数列(そんな言葉があるのかなあ?)としてとらえなければいけないのかなと思います。
つまり、
問題1:T(1,k)
=T(0,1)+T(0,2)+・・・+T(0,k)
=1+1+1+・・・+T(0,k)
(ただし、任意のkについて、T(0,k)=1とする)
問題2:T(2,k)
=T(1,1)+T(1,2)+・・・+T(1,k)
=1+2+3+4+・・・+T(1,k)
問題3:T(3,k)
=T(2,1)+T(2,2)+・・・+T(2,k)
=1+3+6+10+・・・+T(2,k)
問題4:T(4,k)
=T(3,1)+T(3,2)+・・・+T(3,k)
=1+4+10+20+・・・+T(3,k)
問題5:T(5,k)
=T(4,1)+T(4,2)+・・・+T(4,k)
=1+5+15+35+・・・+T(4,k)
問題6:一般に、
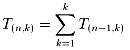
さて改めて、
| 問題1:T(1,k) | =T(0,1)+T(0,2)+・・・+T(0,k) |
| =1+1+1+・・・+T(0,k) | |
| =k |
問題2:
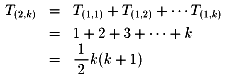
問題3:
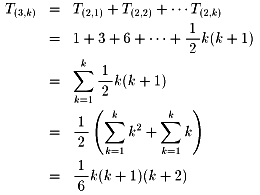
問題4:
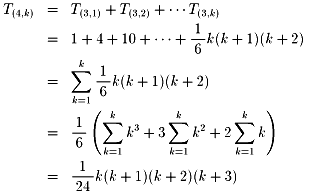
以上のことから、一般に
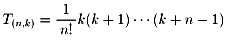
となることが予想されます。

| NO.894 | 2000.11.23. | ねこ | 多項式展開係数(3) |
以下では、Tn=Tn(k)のように書く。
問題1.
T1(k)=1+1+1+1+・・・+1=k
問題2.
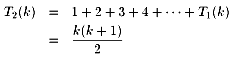
問題3.
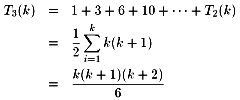
ここで、問題6の解答として次の予想が立つ。
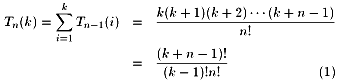
|
(1)が成り立つのを証明する。初めに次の補題を示す。
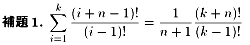
|
証明.帰納法で示す。
i)k=1のとき
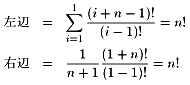
より成立。
ii)k→k+1
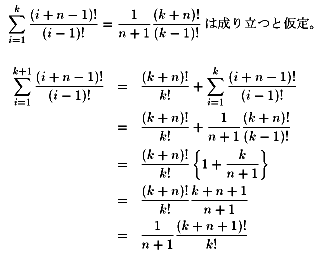
となり成立。
補題1を用いて(1)を証明する。
証明.帰納法で示す。
i)n=1のときは問題1より成立
ii)n→n+1
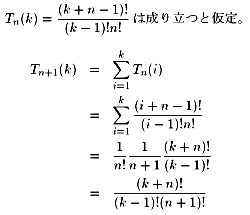
となり、成立。
以上の考察より、以下の解を得る。
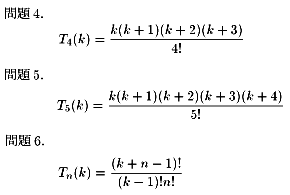
問題7.
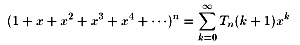
|
証明.帰納法で示す。
i)n=1のとき
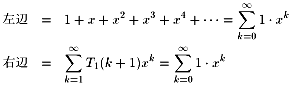
より成立。
ii)n→n+1
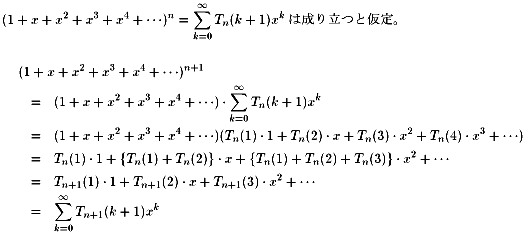
となり、成立。

| NO.895 | 2000.11.26. | 水の流れ | 図形数=m画数 |
太郎さんは、本を読んでいると、図形数=m画数の話がでてきます。
古くは、ピタゴラスとその学派に人々が研究した最初に人々であった。
ここでは、図形数の数列の一般項を考えてみます。
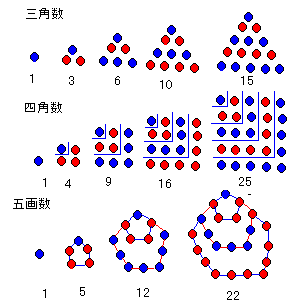
『1』三角数:下の図のように○を並べると、
1,3,6,10,15,・・・という数列ができます。
このように正三角形をなす数を三角数と呼び、
第n番目の三角数をS(3,n)と書くことにします。
『2』四角数:下の図のように○を並べると、
1,4,9,16,25,・・・という数列ができます。
このように正方形をなす数を四角数と呼び、
第n番目の四角数をS(4,n)と書くことにします。
この四角数は別名平方数とも言います。
『3』五角数:下の図のように○を並べると、
1,5,12,22,35,・・・という数列ができます。
このように正五角形をなす数を五角数と呼び、
第n番目の五角数をS(5,n)と書くことにします。
『4』六角数:1,6,15,28,45,・・・という数列があります。
これを六角数と呼び、今までと同様に正六角形を順に作ることができます。
この第n番目の六角数をS(6,n)と書くことにします
さて、一般に、m画数:1,m、3m−3,6m−8,・・・という数列が得られます。
これをm画数と呼び、今までと同様に正m角形を順に作ることができます。
この第n番目のm角数をS(m,n)と書くことにします
また、歴史的には、フェルマー(フランス:1601〜1665)が、
バシェ版のディオファントスの【算術】に「すべての自然数はm個のm画数で表される。」
と書き込んでいます。さらに、ドイツの大数学者ガウス(1777〜1855)も彼が19歳の時に
「あらゆる正の整数は高々3個の三角数の和として表される」ことを見つけています。
ここからが、今回の問題です。この数列の一般項をnで表してください。
問題1:S(3,n):1、3,6,10,15,・・・
問題2:S(4,n):1,4,9,16,25,・・・
問題3:S(5,n):1,5,12,22,35,・・・
題4:S(6,n):1,6,15,28,45,・・・
問題5:一般に、S(m,n):1,m、3m−3,6m−8,・・・

| NO.896 | 2000.11.28. | くまごろう | 生徒からの問題 |
生徒からこんな問題を出されました。
| □ | □ | |
| × | □ | |
| □ | □ | |
| + | □ | □ |
| □ | □ | |
上の図の□の中に1〜9の数字を重ならないように並べ正しい計算をしなさい。
但し、0は使用できません。

 E-mail
E-mail
 戻る
戻る